Hnadling long term dependencies
Vanilla RNN의 한계
아래 Vanilla RNN 의 구조를 보자.
각 timestep별로 결과에 얼마나 영향을 주는지 색으로 표현했을때
색이 짙을 수록 역전파 과정에서 피드백 크기가 점점 작아져서 결과에 영향을 거의 안주게 된다.
만약 앞에 입력이 결과에 영향을 줘야하는 경우라면 현재 timestep으로부터 먼 앞에 입력을 기억하고 있지 않다면
Long Term Dependencies problem 이 발생하게 된다.
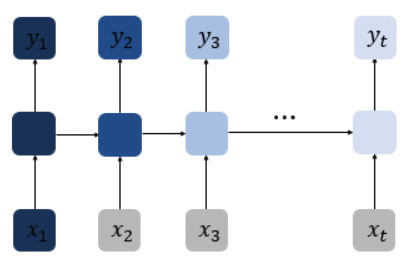
출처: Wiki Docs
\(\begin{align*}\end{align*}\)
자주 사용되는 activation functions
RNN에서 가장 많이 사용되는 activation functions들은 아래와 같다.
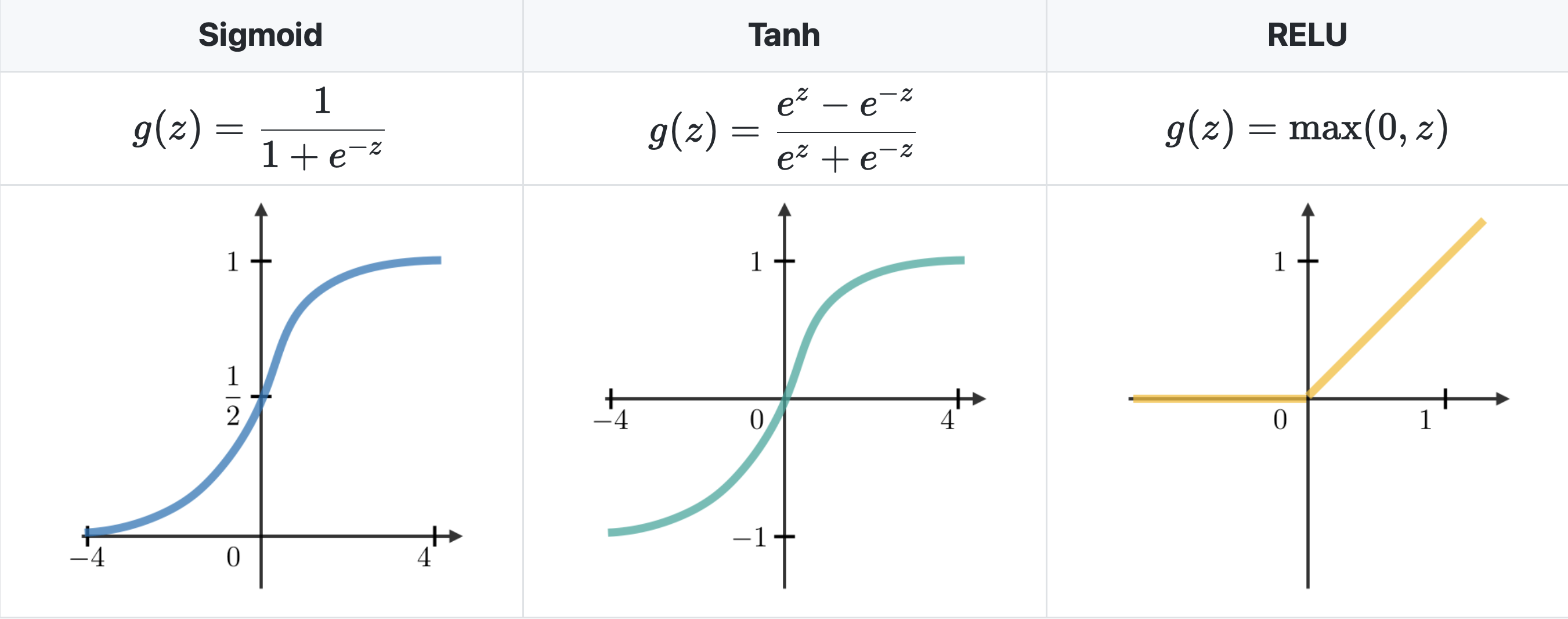
출처: CS 230
\(\begin{align*}\end{align*}\)
Vanishing/exploding gradient
RNN을 사용하다보면 Vanishing/exploding gradient 문제를 자주 만나게 된다.
층의 수에 따라 기하급수적으로 커지거나 작아지는 기울기 때문에
long term dependencies를 포착하기 어려워서
Vanishing/exploding gradient 문제가 발생하게 된다.
\(\begin{align*}\end{align*}\)
Gradient clipping
이 테크닉은 backpropagation 수행중에 가끔 마주치는
exploding gradient 문제에 대응하기 위해 사용된다.
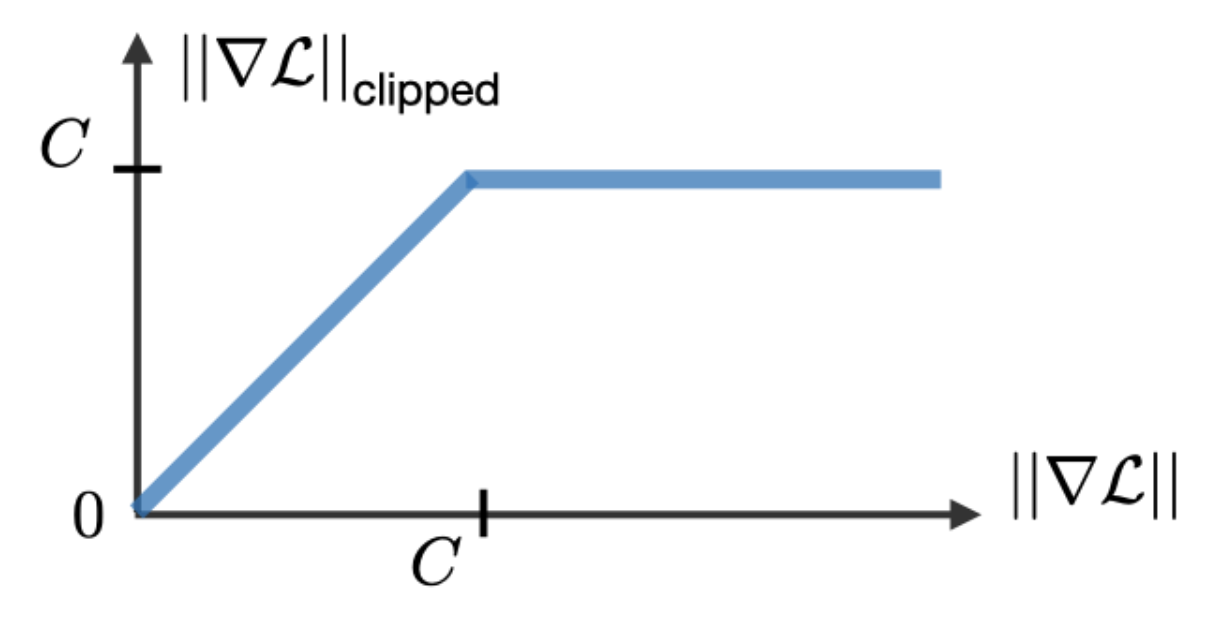
출처: CS 230
\(\begin{align*}\end{align*}\)
GRU/LSTM
Gated Recurrent Unit(GRU)와 GRU의 일반화 버전인 Long Short-Term Memory units(LSTM)은 전통적인 RNNs를 통해 마주하는 vanishing gradient problem을 다루기 위해 사용한다.
\(\begin{align*}\end{align*}\)
Types of Gates
vanishing gradient 문제를 해결하기 위해 RNNs에서는 목적이 잘 정의된 특정 gate들을 사용한다.
그것들을 보통 $\Gamma$ 로 표기한다.
$W,U,b$ 는 gate의 고유한 계수들이고 $\sigma$ 는 sigmoid function이다.
아래는 주요 내용이다.
| Type of gate | Role | Used in |
|---|---|---|
| Update gate $\Gamma_u$ | 과거가 현재에 얼마나 영향을 주는가 | GRU,LSTM |
| Relevance gate $\Gamma_r$ | 이전 정보를 버릴지 | GRU,LSTM |
| Forget gate $\Gamma_f$ | cell을 지울지 말지 | LSTM |
| Output gate $\Gamma_o$ | cell의 어느정도를 내보낼지 | LSTM |
\(\begin{align*}\end{align*}\)
LSTM
LSTM의 cell의 구조는 아래와 같다.
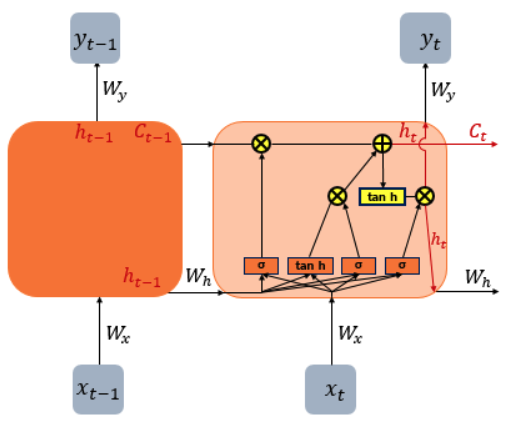
출처 : Explain LSTM & GRU
\[\begin{align*}\\
\text{Input gate}\quad\rightarrow\quad i_t&=\sigma\left(W_{ii}x_t+b_{ii}+W_{hi}h_{t-1}+b_{hi}\right)\\ \\
\text{Forget gate}\quad\rightarrow\quad f_t&=\sigma\left(W_{if}x_t+b_{if}+W_{hf}h_{t-1}+b_{hf} \right)\\ \\
\text{Cell(Gate) gate}\quad\rightarrow\quad g_t&=\tanh\left(W_{ig}x_t+b_{ig}+W_{hg}h_{t-1}+b_{hg} \right)\\ \\
\text{Output gate}\quad\rightarrow\quad o_t&=\sigma\left(W_{io}x_t+b_{io}+W_{ho}h_{t-1}+b_{ho} \right)\\ \\
\text{Cell state}\quad\rightarrow\quad c_t&=f_t\odot c_{t-1}+i_t\odot g_t\\ \\
\text{Hidden state}\quad\rightarrow\quad h_t&=o_t\odot\tanh\left(c_t\right)
\end{align*}\]
\(\begin{align*}\end{align*}\)
GRU
GRU의 cell의 구조는 아래와 같다.
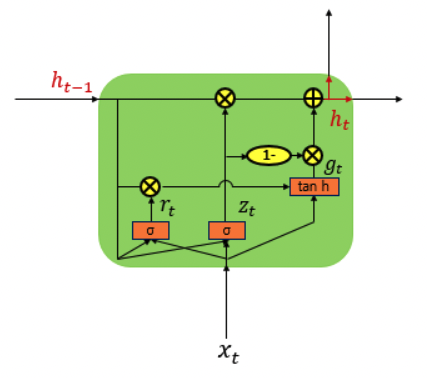
출처 : Explain LSTM & GRU
\[\begin{align*}\\
\text{Reset gate}\quad\rightarrow\quad r_t&=\sigma\left(W_{ir}x_t+b_{ir}+W_{hr}h_{t-1}+b_{hr}\right) \\ \\
\text{Update gate}\quad\rightarrow\quad z_t&=\sigma\left(W_{iz}x_t+b_{iz}+W_{hz}h_{t-1}+b_{hz}\right) \\ \\
\text{New gate}\quad\rightarrow\quad n_t&=\tanh\left(W_{in}x_t+b_{in}+r_t*\left(W_{hn}h_{t-1}+b_{hn}\right)\right) \\ \\
\text{Hidden state}\quad\rightarrow\quad h_t&=\left(1-z_t\right)*n_t+z_t*h_{t-1}
\end{align*}\]
\(\begin{align*}\end{align*}\) \(\begin{align*}\end{align*}\)