RNN Overview

Architecture of a traditional RNN

RNN에서는 은닉층에서 활성화 함수를 통해 결과를 내보내는 역할을 하는 노드를 cell(메모리 셀, RNN 셀) 이라고 한다.

regular feed-forward network에서 hidden layer라고 부르던 뉴런은

RNN에서 hidden state라고 부른다.
\(\begin{align*}\end{align*}\)

hidden state에서는 이전 time step의 hidden state 로부터 얻은 출력값을 현재 time step의 hidden state 에서 입력값으로 사용한다.

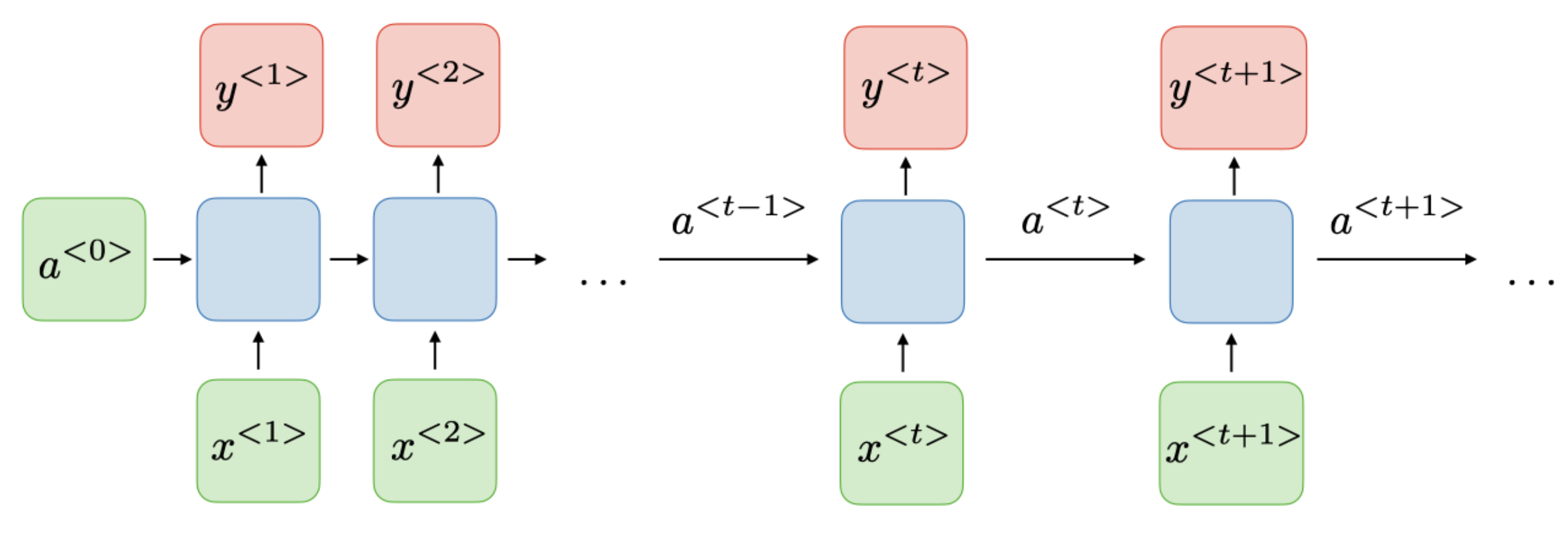
출처: CS 230

timestep $t$ 에서 activation \(a^{<t>}\)와 output \(y^{<t>}\)는 아래와 같이 표현한다.

\[\begin{align*} a^{<t>}&=g_1(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_a)\\ y^{<t>}&=g_2(W_{ya}a^{<t>}+b_y) \end{align*}\]

$W_{ax},\ W_{aa},\ W_{ya},\ b_a,\ b_y$는 모든 timestep에서 변하지 않는 계수이고
$g_1,\ g_2$는 활성함수들이다.
\(\begin{align*}\end{align*}\)

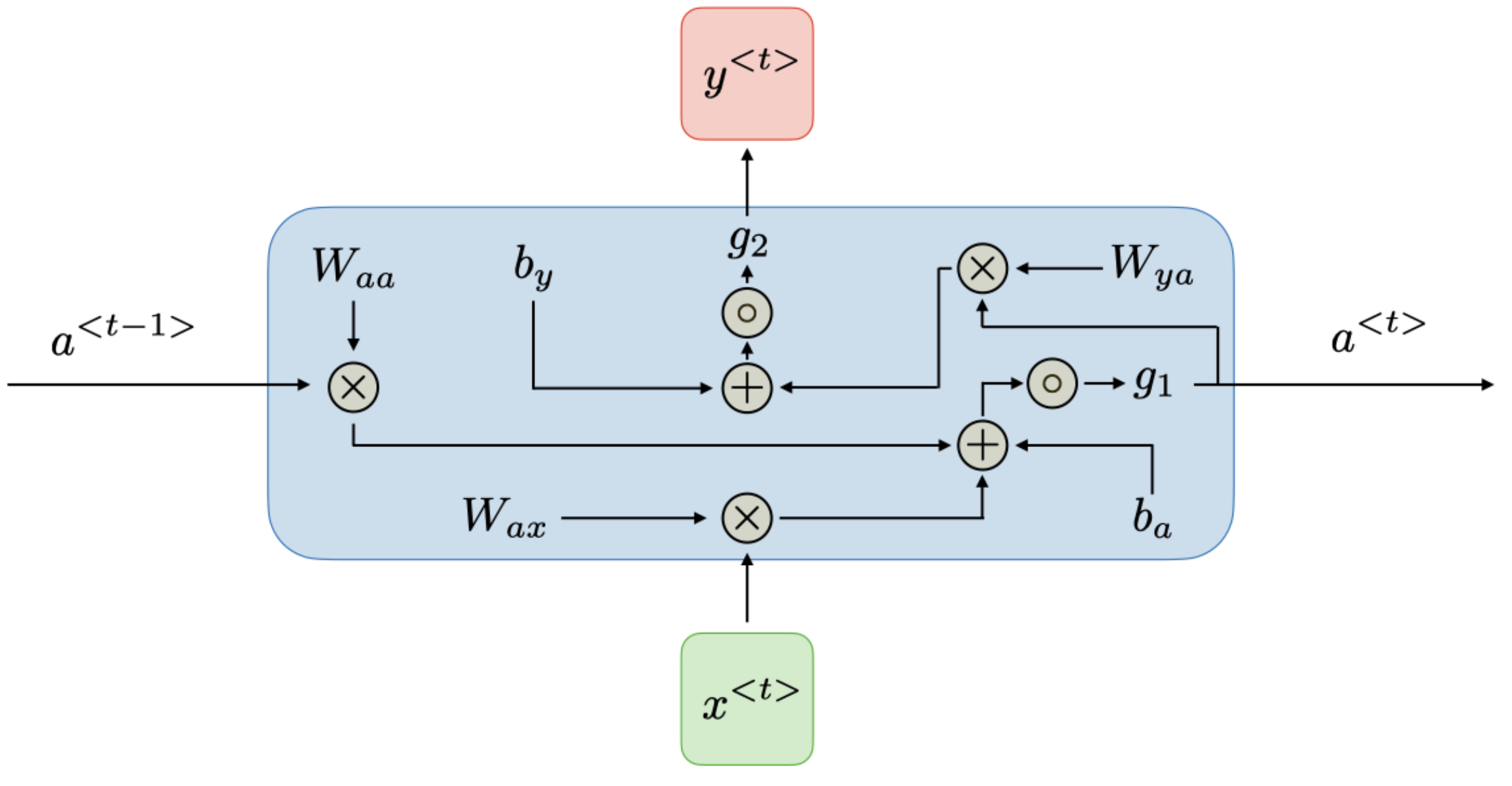
출처: CS 230

RNN의 장점과 단점

Advantages	Drawbacks
$\cdot$ 어떤 길이의 입력도 처리 가능	$\cdot$ 계산이 느림
$\cdot$ 입력 크기에 따라 모델 크기가 커지지 않음	$\cdot$ 오래된 timestep에 접근하기 어려움
$\cdot$ 시간에 대한 결과를 고려한 계산	$\cdot$ 현재 state에서는 미래의 입력을 고려하지 못함
$\cdot$ 전체 시간동안 가중치가 공유됨

\(\begin{align*}\end{align*}\)

Applications of RNNs

RNN model들은 NLP와 speech recognition 처럼 sequential data를 다루기 위해 사용된다.

Type of RNN	Illustration
One-to-one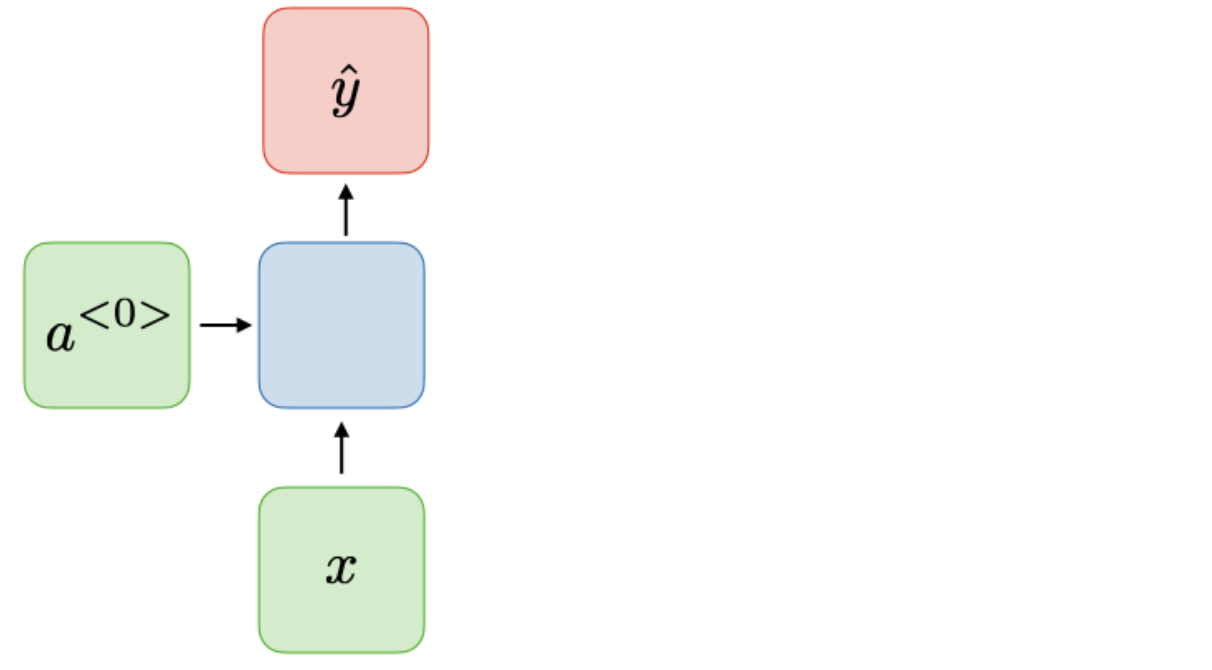
One-to-many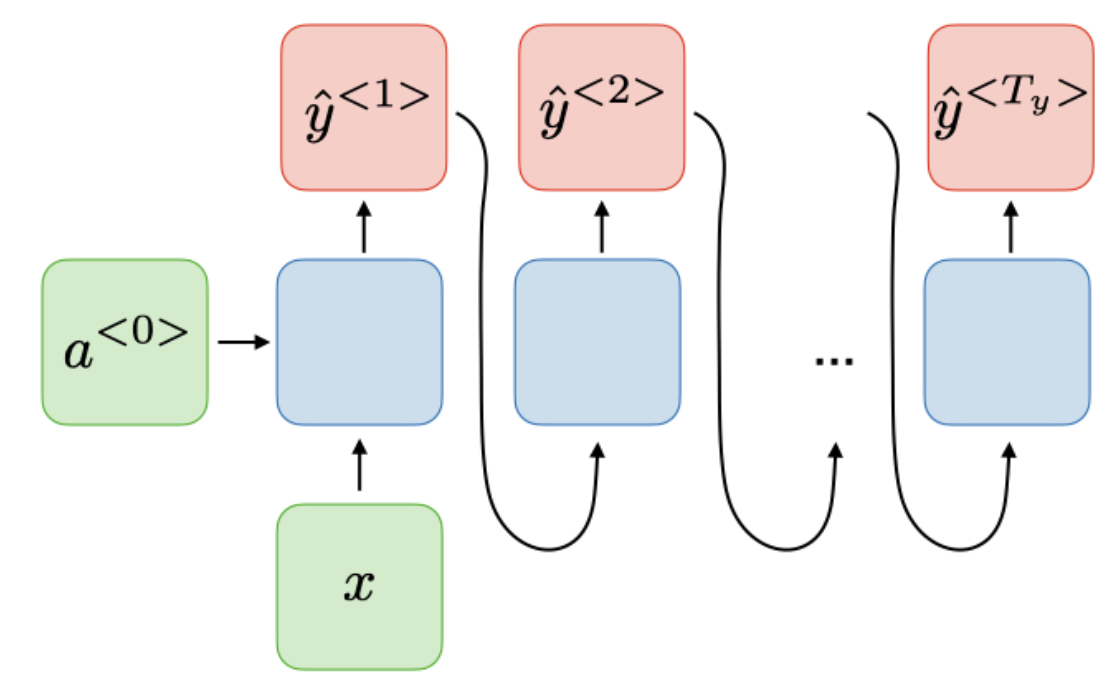
Many-to-one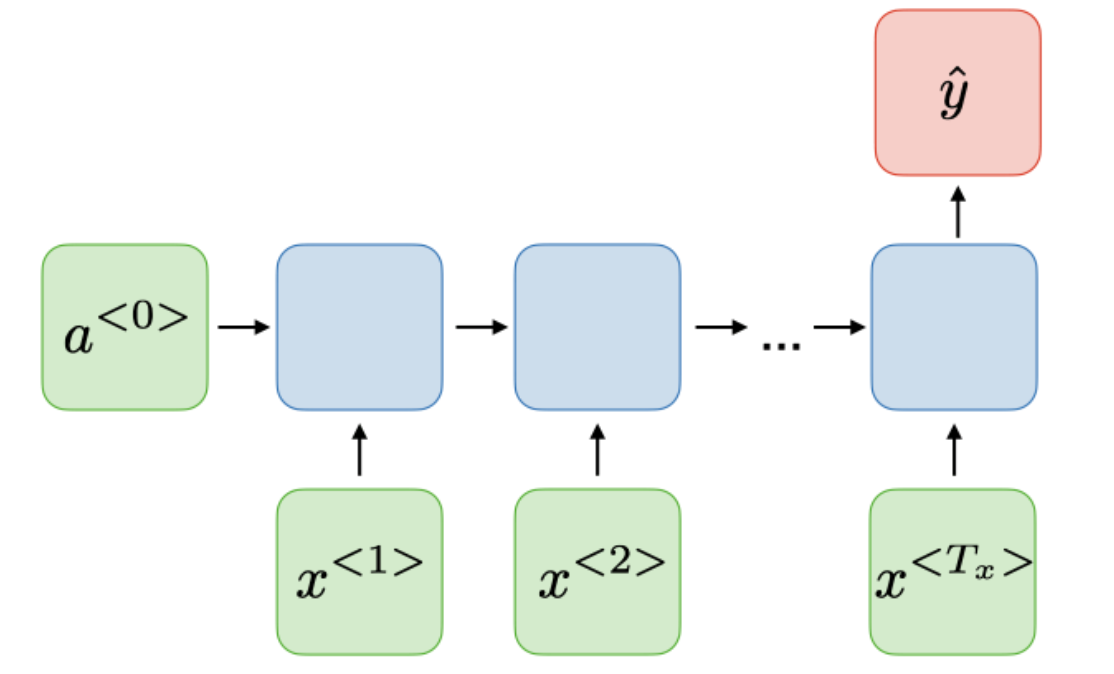
Many-to-many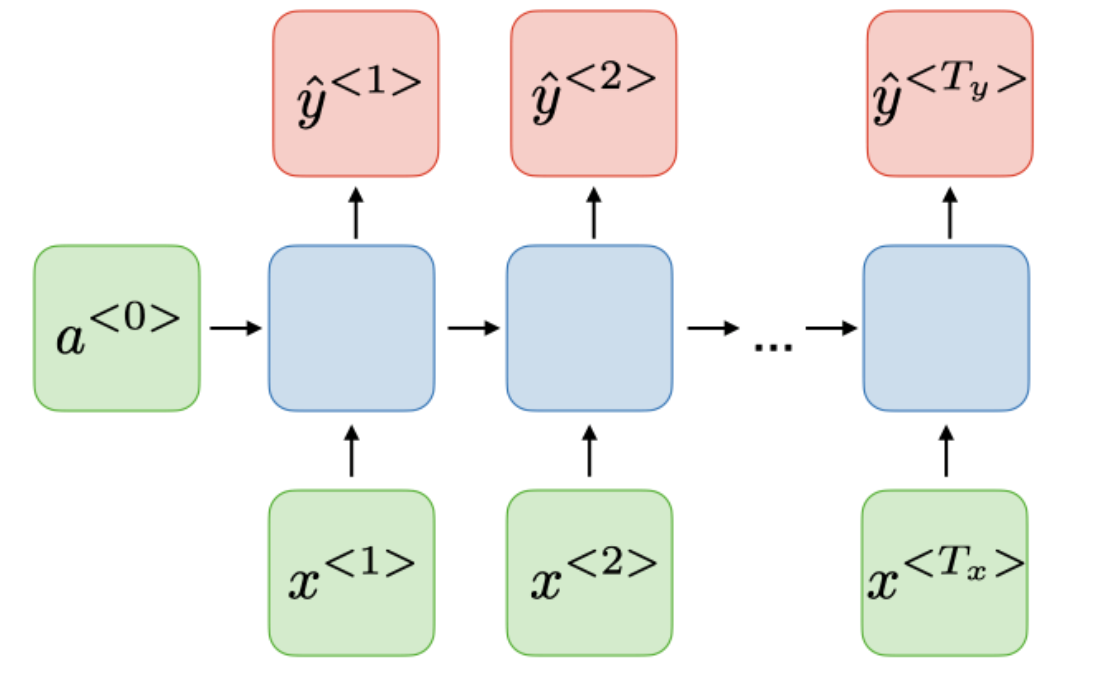
Many-to-many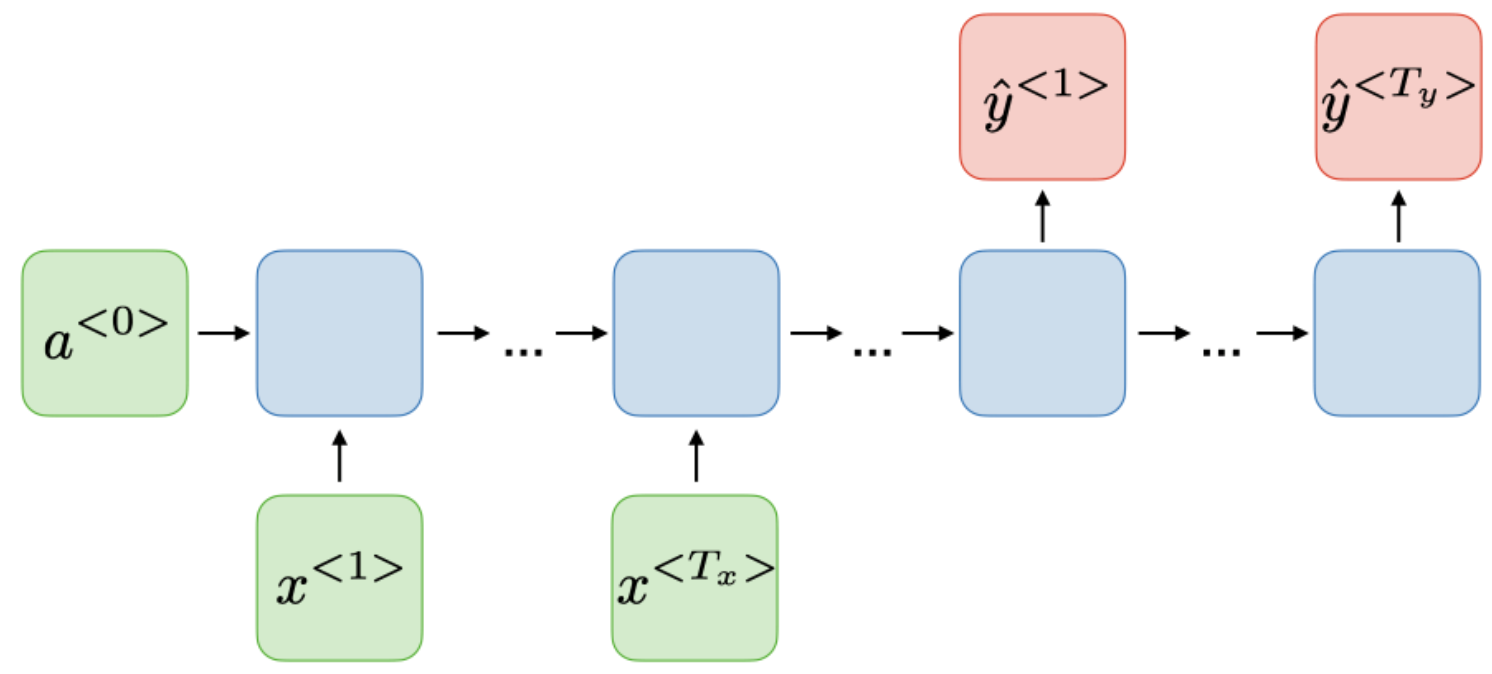

출처: CS 230

\(\begin{align*}\end{align*}\)

Loss function

RNN의 경우 모든 timestep에서 loss function $\mathcal{L}$ 은 각 timestep 별 loss를 더하는 것으로 정의한다.

\[\mathcal{L}(\hat y,y)=\sum\limits^{T_y}_{t=1}\mathcal{L}\left(\hat y^{<t>},y^{<t>}\right)\]

\(\begin{align*}\end{align*}\)

Backpropagation through time

역전파는 각 시간별로 진행된다.
timestep $T$ 인 경우, ${\partial\mathcal{L}^{(T)}\over\partial W}$ 는 아래와 같이 표현된다.

\[{\partial\mathcal{L}^{(T)}\over\partial W}=\left.\sum\limits^{T}_{t=1}{\partial\mathcal{L}^{(T)}\over\partial W}\right|_{(t)}\]

How to do BPTT ?

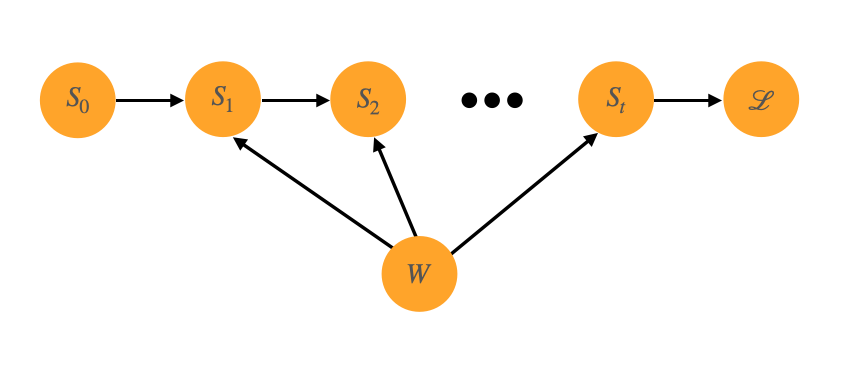예를 들어 위와 같이 $S_t=W\cdot S_{t-1}$ 이고 $\mathcal{L}=W\cdot S_t$ 인 경우
${\partial\ \mathcal{L}\over\partial\ W}$ 는 아래와 같이 구한다.

\[\begin{align*} {\partial\ \mathcal{L}\over\partial\ W}&= {\partial\ \mathcal{L}\over\partial\ S_t}\cdot{\partial\ S_t\over\partial\ W}\\ \\ {\partial\ S_t\over\partial\ W}&= \underbrace{\partial^+\ S_t\over\partial\ W}_{\mathsf{explicit}}+ \underbrace{\dfrac{\partial\ S_t}{\partial\ S_{t-1}}\cdot{\partial\ S_{t-1}\over\partial\ W}}_{\mathsf{implicit}}\\ \\ &= {\partial^+\ S_t\over\partial\ W}+{\partial\ S_t\over\partial\ S_{t-1}}\left[\underbrace{\partial^+\ S_{t-1}\over\partial\ W}_{\mathsf{explicit}}+\underbrace{\dfrac{\partial\ S_{t-1}}{\partial\ S_{t-2}}\cdot{\partial\ S_{t-2}\over\partial\ W}}_{\mathsf{implicit}}\right]=\dots\\ \\ &= {\partial\ S_t\over\partial\ S_t}\ {\partial^+\ S_t\over\partial\ W}+ {\partial\ S_t\over\partial\ S_{t-1}}\ {\partial^+\ S_{t-1}\over\partial\ W}+ {\partial\ S_t\over\partial\ S_{t-1}}\ {\partial\ S_{t-1}\over\partial\ S_{t-2}}\ {\partial^+\ S_{t-2}\over\partial\ W}+\dots+{\partial\ S_t\over\partial\ S_{t-1}}\dots{\partial^+\ S_1\over\partial\ W}\\ \\ &=\sum\limits^t_{k=1}{\partial\ S_t\over\partial\ S_k}\ {\partial^+\ S_k\over\partial\ W}\\ \\ \therefore\dfrac{\partial\ \mathcal{L^{<t>}}}{\partial\ W}&= \dfrac{\partial\ \mathcal{L^{<t>}}}{\partial\ S_t}\ \sum\limits^t_{k=1}{\partial\ S_t\over\partial\ S_k}\ {\partial^+\ S_k\over\partial\ W} \end{align*}\]

위와 같은 개념으로 BPTT 진행하여 RNN이 학습을 한다.

\(\begin{align*}\end{align*}\) \(\begin{align*}\end{align*}\)

참고자료:

Michigan Online,

CS 230,

Wiki Docs

NPTEL-NOC IITM