Recurrent Neural Networks (RNNs):
A gentle Introduction and Overview
Abstract
“Language Modeling & Generating Text”, “Speech Recognition”, “Generating Image Descriptions” or
“Video Tagging” 분야에서 해결책을 위한 최신기술들은 RNN을 기반으로 하고있다.
따라서 현재 또는 앞으로 제시될 해결책들에 대한 구조를 이해하고 따라잡으려면
RNN에 대한 기본 개념을 이해하는 것이 매우 중요할 것이다.
이 논문에서는 BPTT, LSTM 뿐만아니라 Attention Mechanism과 Pointer Networks에 대한 개념을
독자가 쉽게 이해할 수 있도록 가장 중요한 RNN들을 살펴볼 것이다.
그리고 이와 관련해 더 복잡한 주제를 읽어보는 것을 추천한다.
\(\begin{align*}\end{align*}\)
1 Introduction & Notation
RNNs는 sequence data에서 패턴을 찾기위해 주로 사용되는 신경막 구조이다.
Sequence data로는 handwriting, genomes, text 또는 주식시장과 같은 산업에서 만들어지는 numerical time series가 될 수 있다.
그러나, RNNs는 이미지가 패치들로 분해되고 sequence에 따라 적용이 되는 경우에도 적용 된다.
더 높은 수준에서는 RNNs는 Language Modeling & Generating Text, Speech Recognition,
Generating Image Descriptions or Video Tagging 에도 적용된다.
RNN은 MLP라 알려진 Feedforward Neural Networks와 정보가 네트워크를 통과하는 방법에 따라 구분된다.
전방향 네트워크들은 cycle없이 네트워크를 통과시키는 반면,
RNN은 cycle이 있고 정보를 자신에게 다시 전송한다.
이런 방식으로 RNN은 전방향 네트워크의 기능을 확장시켜
현재 입력값 $X_t$ 뿐만 아니라 이전 입력값들 $X_{0:t-1}$을 고려하게 한다.
높은 수준에서 이 차이점을 시각화 한것이 Figure 1이다.
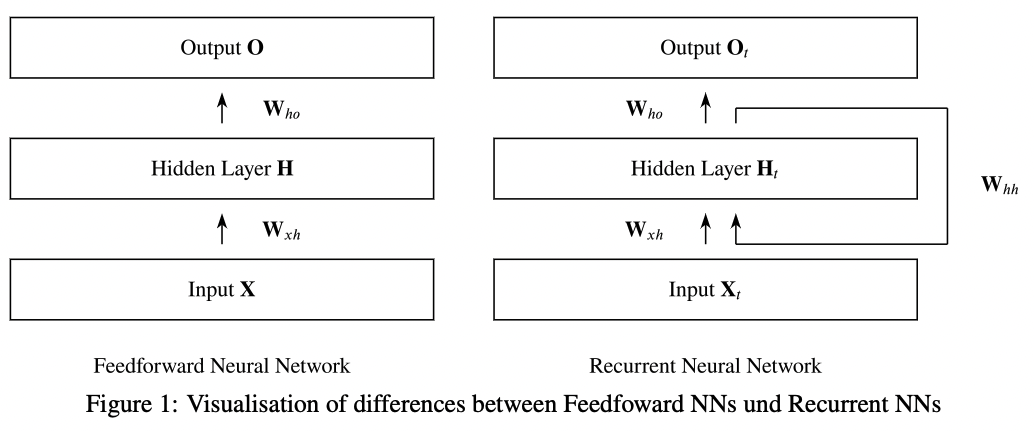
여기서 여러개의 hidden layer를 갖는 옵션은 하나의 Hidden Layer block H를 갖는 것으로 집약된다.
이 block H는 여러개의 hidden layer로 확장될 수 있다.
\(\begin{align*}\end{align*}\)
이전 iteration에서 hidden layer로 정보를 넘기는 과정은 [24]에서 볼 수 있다.
앞으로 time step $t$에 대해 hidden state와 input을
로 표현하고 n은 sample의 개수
d는 각 샘플 별 입력 수
h는 hidden units의 수를 뜻한다.
게다가 가중치 메트릭스로
hidden state to hidden state 메트릭스로
\[W_{hh}\in\mathbb{R}^{h\times h}\]편향으로
\[b_h\in\mathbb{R}^{1\times h}\]마지막으로, activation function을
\[\phi\]로 표현하고 역전파를 사용해 gradient를 구하기 위해 sigmoid나 tanh를 사용한다.
이 표현들을 모두 사용해 만든 식은 hidden variable을 나타내는 Equation 1과
output variable을 나타내는 Equation 2가 있다.
$H_t$가 재귀적으로 $H_{t-1}$을 포함하는 이 과정은 RNN의 모든 time step에서 발생하고
모든 hidden state들을 trace 한다. ($H_{t-1}$과 그 이전 $H_{t-1}$까지 모두)
\(\begin{align*}\end{align*}\)
만약 RNN을 표기했던 방법으로 전방향 신경망을 표기하면
이전 식들과 차이점을 분명하게 알 수 있다.
식3에서 hidden variable을 식4에서는 output variable을 보여준다.
\(\begin{align*}\end{align*}\)
만약 당신이 Feedforward Neural Networks를 학습시키는 기술인 역전파를 잘 알고 있다면
RNN에서 오차를 어떻게 역전파 시킬지에 대한 의문이 생길 것이다.
여기, 이 기술을 Backpropagation Through Time(BPTT)라고 부른다.
\(\begin{align*}\end{align*}\)
2 Backpropagation Through Time(BPTT) &
Truncated BPTT
BPTT는 RNN에 적용된 역전파 알고리즘이다.
이론상 BPTT는 우리가 역전파를 적용 가능하도록 RNN을 펼쳐 전통적인 Feedforward Neural Network와 같은 구조로 만든다.
그러기 위해서, 우리는 이전에 말했던 표기법을 사용한다.
\(\begin{align*}\end{align*}\)
입력값 $X_t$를 네트워크에서 forward pass하는 경우
hidden state $H_t$와 output state $O_t$를 한 step에 모두 계산한다.
그리고 나서 우리는 output $O_t$와 $Y_t$의 차이를 Loss function $\mathcal{L}\left(O,Y\right)$로 아래 식5와 같이 정의할 수 있다.
기본적으로 지금까지 모든 loss term $\ell_t$을 더하여 계산한다.
이 loss term $\ell_t$은 특정 문제에 따라 다르게 정의될 수 있다.
(e.g. Mean Squared Error, Hinge Loss, Cross Entropy Loss, etc.)
우리는 세개의 가중치 메트릭스 $W_{xh}, W_{hh} and W_{ho}$를 사용하기 때문에
각 가중치 메트릭스별로 partial derivative를 계산해야 한다.
평범한 역전파에도 사용되는 연쇄법칙(Chain rule)에 의해 식6로 $W_{ho}$를 구할 수 있다.
$W_{hh}$에 대한 partial derivative는 아래 식7을 통해 계산한다.
\[\begin{align} \dfrac{\partial\ \mathcal{L}}{\partial\ W_{hh}}= \sum\limits^T_{t=1}\dfrac{\partial\ \ell_t}{\partial\ O_t}\cdot\dfrac{\partial\ O_t}{\partial\ \phi_o}\cdot\dfrac{\partial\ \phi_o}{\partial\ H_t}\cdot\dfrac{\partial H_t}{\partial\ \phi_h}\cdot\dfrac{\partial\ \phi_h}{\partial\ W_{hh}}= \sum\limits^T_{t=1}\dfrac{\partial\ \ell_t}{\partial\ O_t}\cdot\dfrac{\partial\ O_t}{\partial\ \phi_o}\cdot W_{ho}\cdot\dfrac{\partial H_t}{\partial\ \phi_h}\cdot\dfrac{\partial\ \phi_h}{\partial\ W_{hh}} \end{align}\]$W_{xh}$에 대한 partial derivative는 아래 식8을 통해 계산한다.
\[\begin{align} \dfrac{\partial\ \mathcal{L}}{\partial\ W_{xh}}= \sum\limits^T_{t=1}\dfrac{\partial\ \ell_t}{\partial\ O_t}\cdot\dfrac{\partial\ O_t}{\partial\ \phi_o}\cdot\dfrac{\partial\ \phi_o}{\partial\ H_t}\cdot\dfrac{\partial H_t}{\partial\ \phi_h}\cdot\dfrac{\partial\ \phi_h}{\partial\ W_{xh}}= \sum\limits^T_{t=1}\dfrac{\partial\ \ell_t}{\partial\ O_t}\cdot\dfrac{\partial\ O_t}{\partial\ \phi_o}\cdot W_{ho}\cdot\dfrac{\partial H_t}{\partial\ \phi_h}\cdot\dfrac{\partial\ \phi_h}{\partial\ W_{xh}} \end{align}\]각 $H_t$가 이전 time step에 의존하기 때문에
식8의 마지막 부분을 아래 식9와 식10으로 대체할 수 있다.
개조된 부분은 아래와 같이 식11과 식12로 쓸 수 있다.
\[\begin{align} \dfrac{\partial\ \mathcal{L}}{\partial\ W_{hh}}= \sum\limits^T_{t=1}\dfrac{\partial\ \ell_t}{\partial\ O_t}\cdot\dfrac{\partial\ O_t}{\partial\ \phi_o}\cdot W_{ho}\sum\limits^t_{k=1}\left(W_{hh}^T\right)^{t-k}\cdot H_k\\ \dfrac{\partial\ \mathcal{L}}{\partial\ W_{xh}}= \sum\limits^T_{t=1}\dfrac{\partial\ \ell_t}{\partial\ O_t}\cdot\dfrac{\partial\ O_t}{\partial\ \phi_o}\cdot W_{ho}\sum\limits^t_{k=1}\left(W_{xh}^T\right)^{t-k}\cdot X_k\\ \end{align}\]여기서 각 time step의 loss term인 $\ell_t$를 통해 매우 커질 수 있는 loss function $\mathcal{L}$을 구하기 위해
$W^k_{hh}$를 저장해야한다.
매우 큰 이 수를 위해 사용하는 이 방법은 매우 불안정하다.
왜냐하면 만약 고유값이 1보다 작으면 gradient는 vanish 될거고
만약 고유값이 1보다 크다면 gradient는 diverge할 것이기 때문이다.
이 문제를 풀 수 있는 방법중 하나는 계산 가능한 수준에서 sum을 자르는 것이다.
이걸 Truncated BPTT라고 하는데 이것은 기본적으로
역전파로 돌아갈 수 있는 만큼 gradient의 time step을 제한하여 구현한다.
여기서 Upper bound를 RNN의 window가 고려할 과거의 time step 수를 의미한다고 생각할 수 있을 것이다.
BPTT는 기본적으로 RNN을 펼쳐 각 time step별로 새로운 layer를 만들기 때문에,
이 과정을 hidden layers를 제한하는 것이라고 여길 수도 있을 것이다.
\(\begin{align*}\end{align*}\)
3 Problems of RNNs:
Vanishing & Exploding Gradients
대부분의 신경망들처럼, vanishing 또는 exploding gradient들은 RNN의 주요한 문제점이다.
식9와 식10에서 본 잠재적으로 매우 긴 sequence에 걸친 matrix multiplication인 경우,
gradient값이 1보다 작다면 점점 gradient가 작아져 결국 vanish될 것이고
이것은 현재 time step으로부터 먼 초기 time step의 state가 주는 영향을 무시하게 된다.
마찬가지로 gradient값들이 1보다 크다면 matrix multiplication을 할 때 exploding gradient 현상이 관찰될 것이다.
\(\begin{align*}\end{align*}\)
이 vanishing gradient 문제를 해결하기 위해 고안된 내용이 Long Short Term Memory units(LSTMs)가 된다.
이 접근으로 Vanilla RNN을 뛰어넘는 성능이 다양한 작업에서 가능해졌다.
다음 섹션에서는 LSTMs에 대해 더 깊게 알아보겠다.
\(\begin{align*}\end{align*}\)
4 Long Short-Term Memory Units (LSTMs)
LSTMs는 vanishing gradient 문제를 해결하기 위해 고안되었다.
LSTMSs는 더 지속적인 error를 사용하기 때문에,
RNNs이 긴 time step(1000번이 넘게)동안 학습을 가능하게 한다.
이것을 위해, LSTMs는 구조상 gated cell이라는 것을 사용하여
전통적인 신경망 흐름 바깥에서 정보를 더 저장하도록 한다.
LSTM에서 이것이 작동하기 위해
- output gate $O_t$ : cell의 입력을 읽음
- input gate $I_t$ : cell로 입력된 데이터를 읽음
- forget gate $F_t$ : cell 내용을 reset 함
이 gate들의 계산을 아래 식13,14,15에 정리했다.
\[\begin{align} O_t=\sigma\left(X_tW_{xo}+H_{t-1}W_{ho}+b_o\right)\\ \notag \\ I_t=\sigma\left(X_tW_{xi}+H_{t-1}W_{hi}+b_i\right)\\ \notag \\ F_t=\sigma\left(X_tW_{xf}+H_{t-1}W_{hf}+b_f\right) \end{align}\] \[\begin{align*}\end{align*}\]위 식에서 \(\quad \begin{align*} W_{xi},W_{xf},W_{xo}&\in\mathbb{R}^{d\times h}\\ W_{hi},W_{hf},W_{ho}&\in\mathbb{R}^{h\times h}\\ b_i,b_f,b_o&\in\mathbb{R}^{1\times h} \end{align*} \quad\) 가 가중치와 편향으로 사용되었다.
\(\begin{align*}\end{align*}\) 게다가 sigmoid 함수를 activation 함수 $\sigma$로 사용하여 출력을 0~1로 만들어 결과적으로 0~1의 값을 갖는 벡터로 변환한다.
\(\begin{align*}\end{align*}\)
다음으로, 이전 gate와 비슷한 연산과정을 갖지만 활성함수로 tanh를 사용하여 결과를 -1~1로 만드는
candidate memory cell $\tilde{C_t}\in\mathbb{R}^{n\times h}$이 필요하다.
그리고 이 cell도 자신의 가중치와 편향 $W_{xc}\in\mathbb{R}^{d\times h},\ W_{hc}\in\mathbb{R}^{h\times h},\ b_c\in\mathbb{R}^{1\times h}$을 갖는다.
아래 식16에서 증명하고 Appendix A에서 시각화 했다.
\(\begin{align*}\end{align*}\)
앞서 말한 gate들을 조합하기 위해 지난 메모리 내용인 $C_{t-1}\in\mathbb{R}^{n\times h}$를 사용한다.
이전 메모리 내용 $C_{t-1}$은 우리가 새로운 메모리 내용 $C_t$에 얼마나 옛날 메모리 내용까지 보존시킬 것인지를 조절한다.
이것은 식17에 정리하고 $\odot$은 element-wise multiplication을 뜻한다.
마지막 단계는 hidden state $H_t\in\mathbb{R}^{n\times h}$를 프레임워크에 추가하는 것이고 아래 식18에 정리했다.
\[\begin{align} H_t=O_t\odot\tanh\left(C_t\right) \end{align}\]tanh 함수를 통해 $H_t$의 각 원소들은 -1~1로 정의 될것이고
전체 LSTM 구조는 아래와 같다.
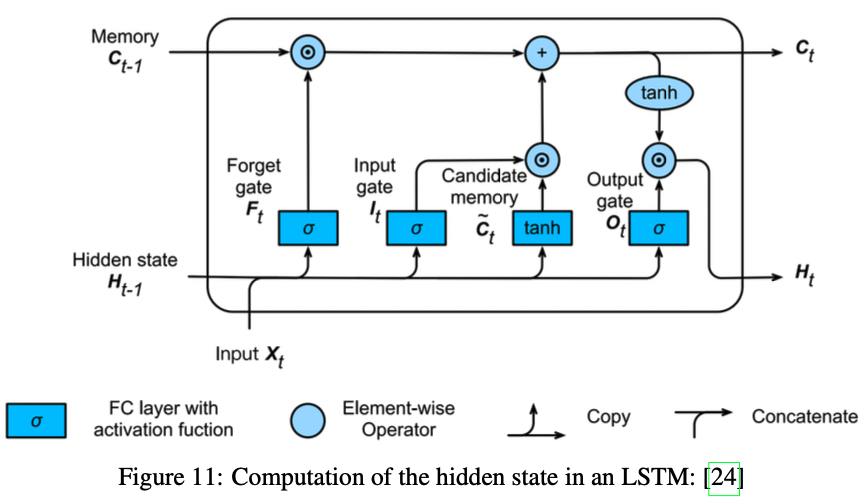
\(\begin{align*}\end{align*}\)
5 Deep Recurrent Neural Networks (DRNNs)
DRRNs는 아주 쉬운 개념이다.
L개의 hidden layers를 갖는 DRNN을 만들려면
아무 타입의 RNNs를 평범하게 쌓아 올리면 된다.
각 hidden state $H_t^{\left(\ell\right)}\in\mathbb{R}^{n\times h}$는 현재 층의 다음 time step인 $H^{\left(\ell\right)}_{t+1}$으로 전달되고
똑같이 현재 time step의 다음 층인 $H^{\left(\ell+1\right)}_t$으로 전달된다.
첫 번째 층을 위해 이전 모델에서 보여준 hidden state 계산을 아래 식19에서 보여준다.
그 다음 층의 경우는 이전 층의 hidden state를 input으로 인식하여 식20을 사용한다.
output $O_t\in\mathbb{R}^{n\times o}$에서 o는 output의 수인데
output은 현재 times step의 마지막 층에 대한 hidden state값만 이용해 계산을 하고 식21에서 보여준다.
\(\begin{align*}\end{align*}\)
6 Bidirectional Recurrent Neural Networks (BRNNs)
일단 language modeling에 대한 예시를 보자.
현재 모델에서는 지금까지 봐온 내용에 근거하여 믿음이 가는 예측을 통해 다음 sequence element(i.e. the next word) 를 알아낸다.
그러나, 문장의 사이 공간을 채우거나 공간 뒤에 문장의 어느 부분을 채우는 경우에 중요한 정보를 전달하게되는데
이 정보는 이런 작업들이 잘 수행되도록 필수적인 역할을 한다.
더 일반적인 수준에서 우리는 sequence의 특성을 미리 보고 지금과 통합하고 싶다.
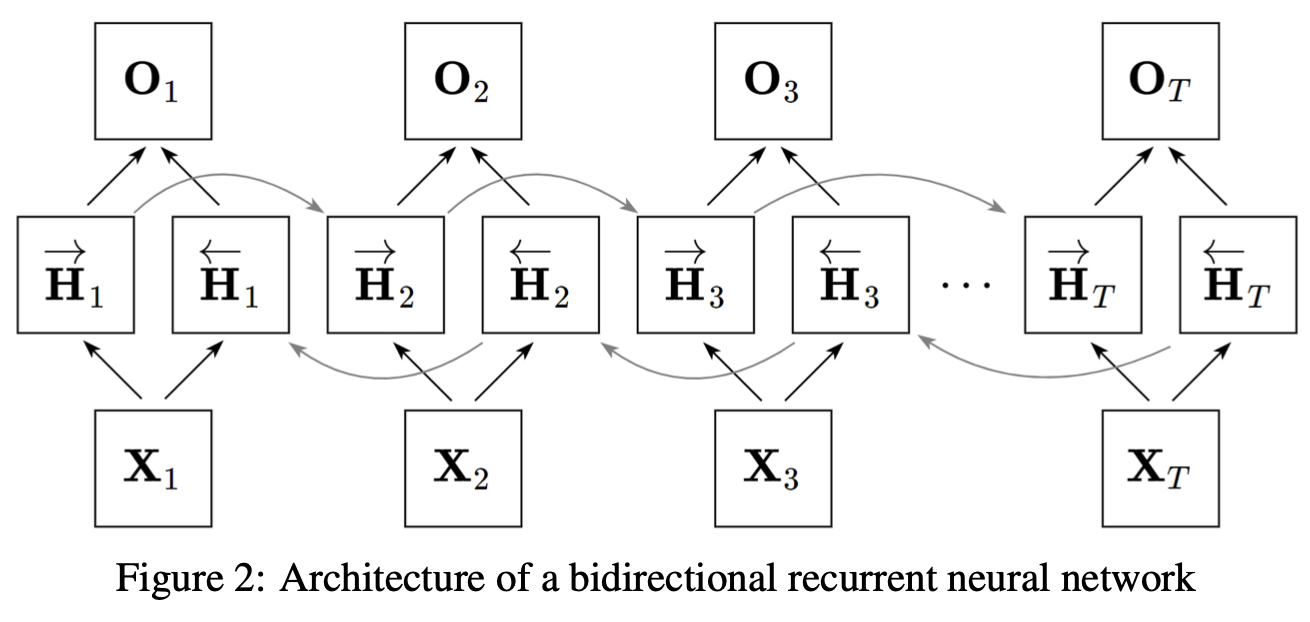
이 미리보는 특성을 달성하기 위해 마지막 element부터 반대방향으로 sequence가 적용되는 hidden layer가 추가된 Bidirectional Recurrent Neural Networks (BRNNs)가 등장한다.
구조를 미리보여주기 위해 위에 Figure2를 삽입했다.
이제 forward hidden state $\overset{\rightarrow}{H_t}\in\mathbb{R}^{n\times h}$와 backward hidden state $\overset{\leftarrow}{H_t}\in\mathbb{R}^{n\times h}$ 를 소개하겠다.
이 두 hidden state는 각각 식22와 식23에 정리했다.
이전까지는 비슷한 가중치 메트릭스를 정의했지만,
지금부터는 두개로 분리된 매트릭스를 정의할 것이다.
하나는 forward hidden states를 위한 것으로 아래와 같이 정의한다.
이것을 통해 결과 o가 output의 수를 뜻하는 $O_t\in\mathbb{R}^{n\times o}$ 를 계산할 수 있게 된다. 여기서 $\frown$은 두 메트릭스를 axis 0으로 concate하는 것을 의미한다.(위 아래로 쌓음)
\[\begin{align} O_t=\phi\left(\left[\overset{\rightarrow}{H_t}\frown\overset{\leftarrow}{H_t}\right]W_{ho}+b_o\right) \end{align}\]다시말하자면, 가중치 매트릭스 $W_{ho}\in\mathbb{R}^{2h\times o},\ b_o\in\mathbb{R}^{1\times o}$를 정의한다.
두 방향은 서로 다른 수의 hidden units를 갖을 수 있다.
\(\begin{align*}\end{align*}\)
7 Encoder-Decoder Architecture &
Sequence to Sequence (seq2seq)
Encoder-Decoder architecture는 네트워크가 두 부분으로 이루어진 신경망 구조이다.
Encoder network는 input을 state로 encoding하고 Decoder network는 state를 output으로 decoding한다.
state는 vector나 tensor의 형태를 보인다.
구조는 Figure3에 있다.

이 Encoder-Decoder 구조에 근거하여
Sequence to Sequence (seq2seq)라고 불리는 모델이
sequence input에 대해 sequence output을 만들어 내도록 제안되었다.
이 모델은 RNNs를 encoder와 decoder에 사용하고
encoder의 hidden state가 decoder의 hidden state로 전달된다.
seq2seq의 일반적인 응용프로그램으로는 Google Translate, voice-enabled devices or labeling video data가 있다.
가장 초점을 두는 것은 고정된 길이의 input sequence size n을 고정된 길이의 output sequence size m으로 맞추는 것이다.
여기서 n과 m은 서로 다른 값일 수도 있지만 반드시 다를 필요은 없다.
\(\begin{align*}\end{align*}\)
제안된 구조를 Figure4에서 시각화 해놨다.
여기서 encoder는 RNN으로 구성되고 single element인 sequence data $X_t$를 사용한다.
$t$는 sequence element의 순서를 뜻한다.
사용되는 RNNdms LSTM이나 GRU가 성능을 향상시키기 위해 사용된다.
게다가, hidden state $H_t$는 LSTM이나 GRU같은 RNN에 사용되는 hidden state계산과정과 같은 방법으로 계산된다.
Encoder Vector(context)는 encoder network의 마지막 hidden state로 이전 input element들의 모든 정보를 통합하는 목적을 갖는다.
Encoder Vector는 decoder network의 첫 번째 hidden state 역할을 하고
decoder가 정확한 예측이 가능하게 한다.
Decoder network는 RNN으로 설계되었고 time step $t$에서 output $Y_t$ 를 예측한다.
만들어진 output은 또 다시 sequence이며 $t$에 대한 순차를 가진 $Y_t$가 된다.
각 time step에서 RNN은 이전 unit 으로부터 hidden state를 수용하고
자신으로부터 output과 new hidden state를 만들어낸다.
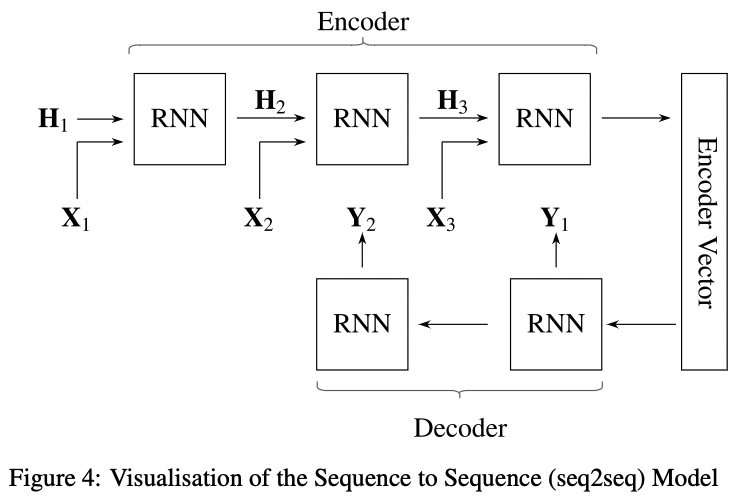
고정된 길이의 vector인 source sentence의 모든 정보를 포함할 필요가 있기 때문에
Encoder Vector가 특히 long sequences를 입력 받게 되면 위와 같은 구조에서는 병목현상이 발생하게 된다.
이러한 문제를 해결하기 위해 Attention을 사용해 해결을 하고있다.
다음 장에서는, 그에 대한 해결책을 살펴보겠다.
\(\begin{align*}\end{align*}\)
8 Attention Mechanism & Transformer
RNNs을 위한 Attention Mechanism는 부분적으로 human visual focus와 Peripheral perception으로부터 영감을 받았다.
이것은 사람이 특정지역에 초점을 두고 고해상도로 인식을 하게 하고
주변 객체들은 저해상도로 인식하게 한다.
이 focus points와 adjacent perception을 기반으로,
사람은 자신이 focus point를 변경할 때 무엇을 인지 해야하는지 추측할 수 있게 된다고 한다.
비슷하게, 이 방법을 단어들의 sequene로 관찰된 단어들 중에서 추론이 가능하도록 변형시킬 수 있다.
예를들어, 만약 우리가 eating이라는 단어를 “She is eating a green apple”이라는 sequence에서 인지한다면,
가까운 미래에 음식이라는 객체를 찾을 것이다.
\(\begin{align*}\end{align*}\)
일반적으로, Attention은 두 문장을 받고 그들을 단어가 row나 column의 요소로 이루어진 메트릭스로 변형시킨다.
이 matrix layout을 기반으로 비슷한 맥락을 식별하거나 그들 사이에 연관성을 식별해 matrix를 채운다.
이 내용에 대한 예제를 Figure5에서 볼 수 있다.
Figure5는 높은 연관성을 흰색으로 낮은 연관성을 검은색으로 표현한다.

\(\begin{align*}\end{align*}\)
8.1 Definition
seq2seq 모델이 long sequences를 더 잘 다루도록 하기 위해 attention mechanism이 등장한다.
encoder network의 마지막 hidden state의 결과로 Encoder Vector를 만드는 대신에,
attention은 context vector와 전체 입력 source 사이에 shortcut을 사용한다.
이 과정을 시각화 하면 Figure6가 된다.
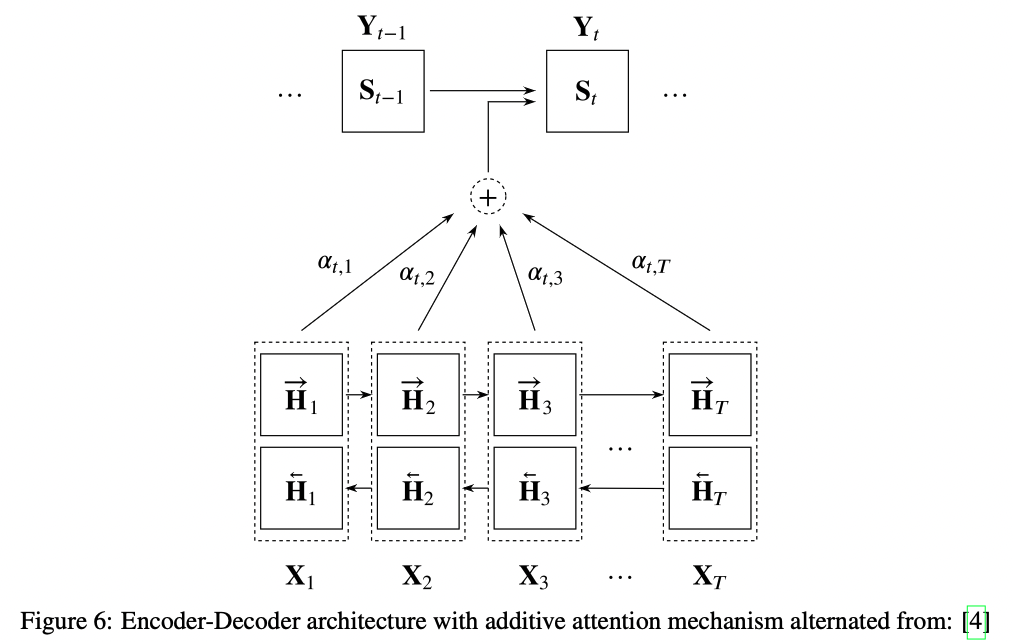
여기서 n만큼의 길이를 가진 source sequence X를 갖고
m의 크기를 갖는 target sequence Y를 결과로 얻으려고 한다.
그런 점에서 그 식은 7장에서 앞서 말한 내용과 유사하다.
식25처럼 forward와 backward 방향을 concate한 전반적인 hidden state $H_{t’}$ 를 갖는다.
또한, decoder network의 hidden state는 $S_t$로 표기하고
encoder vector는 $C_t$로 표기하며 이 둘은 식26과 식27에서 정리했다.
context vector $C_t$는 intput sequence의 hidden state들의 가중치 합이다.
여기서 가중치인 alignment score $\alpha_{t,t’}$는
$\sum\limits^T_{t’=1}\alpha_{t,t’}=1$을 만족한다.
alignment $\alpha_{t,t’}$는 intput 위치 $t’$와 output 위치 $t$의 alignment score 연결한다.
이 score는 가리키는 쌍이 얼마나 잘 맞는지를 나타낸다.
모든 alignment score의 집합은 각 source hidden state가 각 output에 얼만큼 고려되었는지를 정의한다.
Apeendix B에서 더 쉽고 시각화된 seq2seq에 대한 attention mechanism 설명을 보면 좋을것이다.
\(\begin{align*}\end{align*}\)
8.2 Diffrent types of score functions
일반적으로, score function은 다양한 작업에서 사용될 때 여러가지 방법으로 구현된다.
Table 1은 이름, 식과 사용에 따라 정리한것이다.
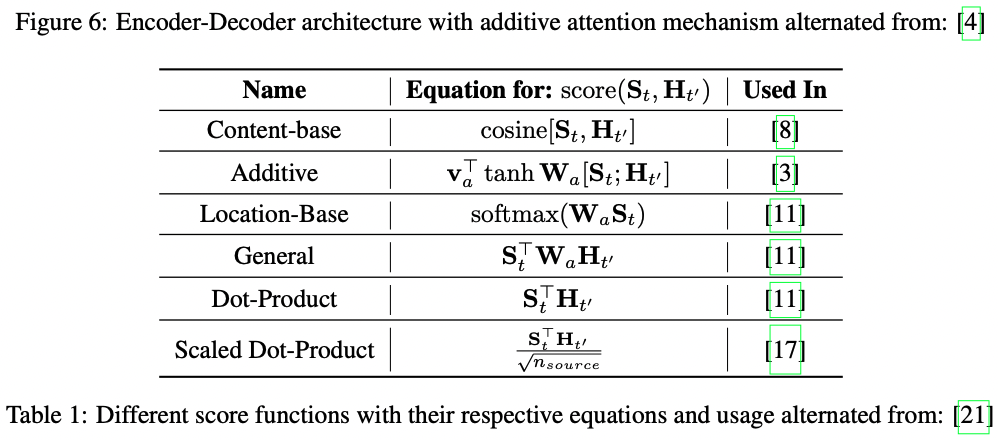
여기 alignmnet 모델에 두개의 학습 가능한 가중치 메트릭스 $\mathbf{v}_a$와 $W_a$가 있다고 하자.
Scaled-Dot-Product 는 입력이 큰 경우 softmax 함수의 gradient가 매우 작아져서
효율적인 학습에 문제가 생기는 점에서 영감을 얻어서 현재 순서의 단어의 글자수를 곱셈에 이용한다.
\(\begin{align*}\end{align*}\)
8.3 Transformer
Attentions Mechanism을 통합함으로써 Transformer가 등장한다.
Transformer는 recurrence sequence를 attention으로 병렬화 하지만
동시에 sequence에서 각 아이템의 위치를 encoder-decoder 구조를 통해 encoding한다.
사실, 그러기 위해서는 RNNs를 쓰지 않고 성능 향상을 위해
전적으로 self-attention을 사용한다.
구조상 encoding하는 부분은 몇가지 encoder들로 만들어지고
decoder 부분은 encoder 부분과 같은 수의 decoder들로 만든다.
구조를 일반화 한 사진은 Figure7과 같다.
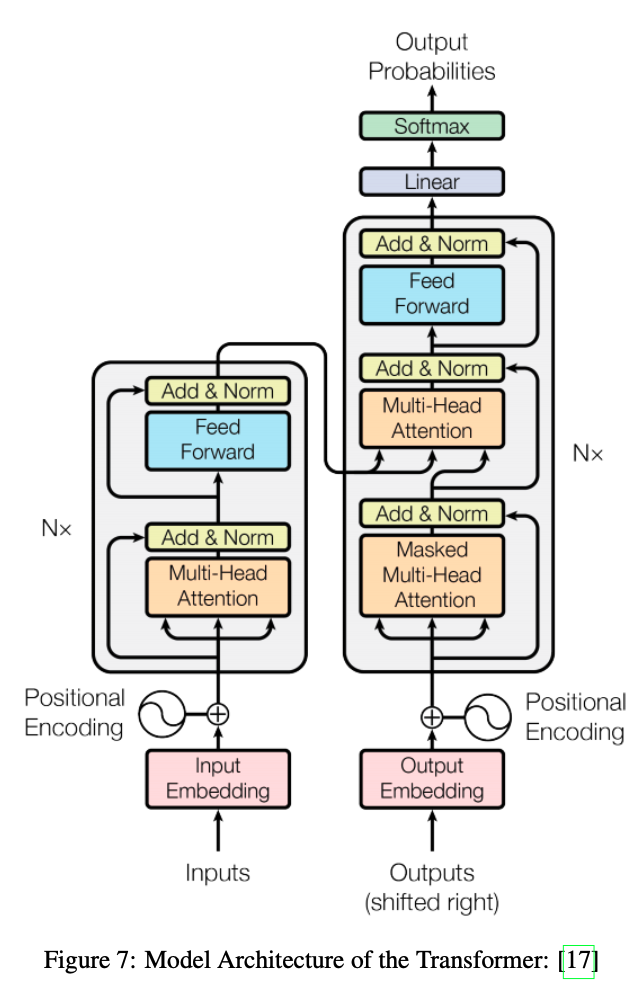
여기서, 각 encoder의 구성요소는 Self-Attention과 FeedForward Neural Network로 이루어진 2개의 하위 계층을 가진 구조로 이루어져있다.
비슷하게, 두 하위 계층은 각 decoder 구성요소에서도 발견되지만
Encoder-Decoder Attention에서 둘 사이에 하위 계층은 seq2seq에 사용된 Attention과 비슷한 일을 한다.
배치된 Attention 계층들은 평범한 attention 계층들이 아니니라 Multi-Headed Attention으로 attention 계층의 성능을 향상시킨다.
Multi-Headed Attention은 모델이 다른 위치에서 다르게 표현한 내용으로부터 정보를 읽게 한다.
쉽게 말해 병렬 구조에서 다른 블락에서 작동하고 결과를 concate한다는 것이다.
불행하게도, multi-head attention의 설계적 선택과 수학적 공식에 대한 설명을 포함하는 것은 이 논문에서 너무 지나친 내용일 수 있다.
더 많은 내용을 원한다면 밑에 참고문서를 봐라.
Figure7에서 보인 구조는 encoder와 decoder 모두에 skip connections과 각 하위 계층에 normalisation 계층을 배치했다.
한가지 중요한 것은 입력과 결과 모두 embedding되고
positional encoding은 sequence element들의 가까운 정도를 표현하도록 적용되었다는 것이다.
\(\begin{align*}\end{align*}\)
마지막 linear와 softmax 층은 decoder stack을 단어로 결과를 만들어 실수 타입의 vector를 반환한다.
이것은 linear 계층을 통해 vector를 훨씬 더 큰 logits vector로 변환함으로써 완성된다.
이 logits vector는 각 cell이 고유한 단어에 대한 점수를 뜻하는 학습 데이터셋을 통해 학습된 어휘의 크기를 갖는다.
softmax를 적용함으로써 그들의 점수를 확률값으로 반환하고
특정 time step에 대해 가장 확률값이 큰 결과로써 cell(i.e. the word)을 선택할 수 있다.
\(\begin{align*}\end{align*}\)
9 Pointer Networks(Ptr-Nets)
Pointer Networks(Ptr-Nets)는 결과 dictionary에 우선순위의 분산된 범주를 고치지 않음으로써 attention과 seq2seq를 적용해 개선시켰다.
input sequence로부터 output sequence가 산출되는 대신에,
pointer network는 input series의 요소들에 단계적으로 pointer가 적용되도록 한다.
한 논문에서는 Pointer Network를 사용해 computing planar convex hulls,
Delaunay triangulations and the symmetric planar Travelling Salesman Problem(TSP)문제를 해결할 수 있다고 증명했다.
일반적으로 state사이에 추가적인 attention을 적용하고나서
softmax를 통해 모델의 결과가 확률값을 갖도록 normalize한다(식29).
Ptr-Net이 encoder state들을 attention weights가 적용된 output과 섞이지 않게 해서
attention mechanism을 단순화시킨다.
이 방법에서는 output이 위치에 대한 정보에만 반응하고 input content에 의해서는 반응하지 않는다.
\(\begin{align*}\end{align*}\)
10 Conclusion & Outlook
이 논문에서는 기본적인 RNNs를 설명한다.
일반적인 RNNs의 프레임워크, BPTT, RNNs의 고질적인 문제점, LSTM, DRNNs, BRNNs와 가장 최근 연구된 Encoder Decoder Architecture와 seq2seq 모델 그리고 Attention과 Transformer와 Pointer Network에 대한 내용을 포함한다.
대부분의 주제들은 개념적으로만 다루고 구현적 특성을 다루지는 않았다.
여기서 다룬 주제들에 대한 더 넓은 이해를 하려면 original 논문을 보도록 해라.
추가적으로 가장 최근 출판된 논문에서는 최근 개념들을 다루니까 더욱 원래 논문을 보기를 권한다.
\(\begin{align*}\end{align*}\)
최근 출판된 논문들중 하나는 제시된 개념들을 많이 사용한다.
“Grandmaster level in StarCraft2 using multi-agent reinforcement learning”이라는 논문이고 Vinyals가 썼다.
여기에서, 그들은 agent를 실시간으로 전략 게임 StarCraft2를 훌륭하게 학습시키는 접근 방법을 제시한다.
만약 제시된 내용들이 다소 이론적이라면 실제 환경에 적합하도록 설정되어 배포된 LSTM, Transformer와 Pointer Networks에 관한 논문을 읽어보기를 권한다.