VGGNet

VGGNet

1. Introduction

합성곱 네트워크는 최근(2015) 대규모 공공 이미지 저장소인 ImageNet과 고성능 계산 시스템(GPU)와 대규모 cluster 덕분에 큰 규모의 이미지나 비디오 인식에 좋은 성과를 보인다.

특히, ILSVRC는 deep visual recognition 구조들의 진보에서 중요한 역할을 했다.

ILSVRC는 고차원 얕은 특징 인고딩에서 심층 ConvNet에 이르기까지 몇 세대에 걸친 대규모 이미지 분류 시스템의 테스트베드 역할을 했다.

ConvNet들이 computer vision 분야에서 점점 상품화 되면서 더 높은 정확도를 달성하기위해 Krizhevsky의 original 구조(AlexNet)를 개선하려고 많은 시도들이 있었다.

예를들어, ILSVRC-2013에서 최고의 성능은 Alexnet에서 receptive window의 크기를 줄이고 첫 번째 합성곱층에서 더 작은 stride를 사용해서 얻은 모델로부터 얻어졌다.

다른 라인에 대한 개선은 모델이 전체 이미지나 크기가 변형된 이미지를 더 조밀하게 학습하고 시험하게 했다.

이 논문에서, 우리는 ConvNet구조에서 또 다른 중요한 측면인 깊이에 대해 알아볼 것이다.

논문 끝에는, 구조의 다른 매개변수들을 고정시키고 모든 층에서 합성곱 필터의 크기를 3x3으로 작게 설정하게 해서 합성곱층을 더 많이 추가하여 깊이를 꾸준히 증가시켜볼 것이다.

결과적으로, ILSVRC classification과 localisation작업에서 최첨단 모델의 정확도를 달성할 뿐 아니라 간단한 파이프라인에 사용되더라도 다른 이미지 데이터에 대해 적용했을 때 최고의 성능을 보이는 상당히 정확한 ConvNet 구조를 만들었다.

우리는 연구를 통해 얻은 가장 좋은 성능의 두가지 모델을 후속연구를 위해 공개했다.

다음장에서는 ConvNet 구성을 묘사하고 3장에서는 image classification training과 evaluation에 대한 내용을 설명하고 4장에서는 ILSVRC classification작업에서 configuration들을 비교하고 5장에서는 결론을 내렸다.

ILSVRC-2014 object localisation system을 Appendix A에서 묘사하고 평가했다 Appendix B에서는 very deep features 의 generalisation에대해 논의하고 Appendix C에서는 주요 논문에 대한 개정 내용이 포함된다.

2. ConvNet Configurations

같은 조건에서 ConvNet depth의 증가가 가져오는 개선을 측정하려면 설계에 사용된 모든 ConvNet 층의 구성에 Ciresan과 Krizhevsky와 동일한 조건들을 적용해야 한다.

2장에서는 먼저 ConvNet 구성에서 일반적인 내용을 서술하고 그다음 평가에서 사용된 특정한 configuration에 대해 자세하게 서술한다.

마지막으로 설계할 때 했던 선택들을 이전 최신기술과 비교해볼것이다.

2.1 Architecture

학습하는 동안, ConvNet의 입력값은 224x224x3 형태이다.

각 픽셀로부터 training set에서 계산한 평균 RGB값을 빼주는 전처리 이외에 다른 전처리는 하지 않았다.

양옆과 위아래에 대한 정보를 담을 수 있는 가장 작은 사이즈인 3x3의 매우 작은 receptive field를 가지는 필터를 사용한 합성곱층의 stack에 이미지를 통과 시켰다.

우리는 non-linearity를 따르는 1x1 합성곱 필터 또한 사용했다.

합성곱의 stride는 1 pixel로 고정했다; convolution 연산 후에 입력과 같은 모양이 나오도록 padding은 1 pixel을 사용했다.

Spatial pooling은 합성곱 뒤에(모든 합성곱은 아님) 5개의 max-pooling층으로 수행된다.

Max-pooling은 2x2 pixel window가 stride=2의 값으로 연산을 한다.

모델별로 다른 깊이를 적용해서 만든 stack of convolutional layers 뒤에는 전결합층이 나온다.

처음 두개의 전결합층은 각각 4096개의 유닛을 가지고 세 번째 전결합층은 1000개의 유닛을 갖는다.

마지막층은 SoftMax층이다.

전결합층들의 구성은 모든 네트워크들이 같도록 설계했다.

모든 은닉층들은 ReLU non-linearity를 사용한다.

이번 연구의 네트워크들은 한 개를 제외하고 AlexNet에서 사용된 Local Response Normalisation(LRN) 을 사용하지 않았다 : LRN은 ILSVRC 데이터 셋에서의 성능을 개선시키지 못하면서 메모리 사용량은 증가시키고 계산시간도 증가시켰다.

LRN이 적용된 경우 LRN층의 매개변수들은 AlexNet의 LRN층의 매개변수와 같다.

2.2 Configurations

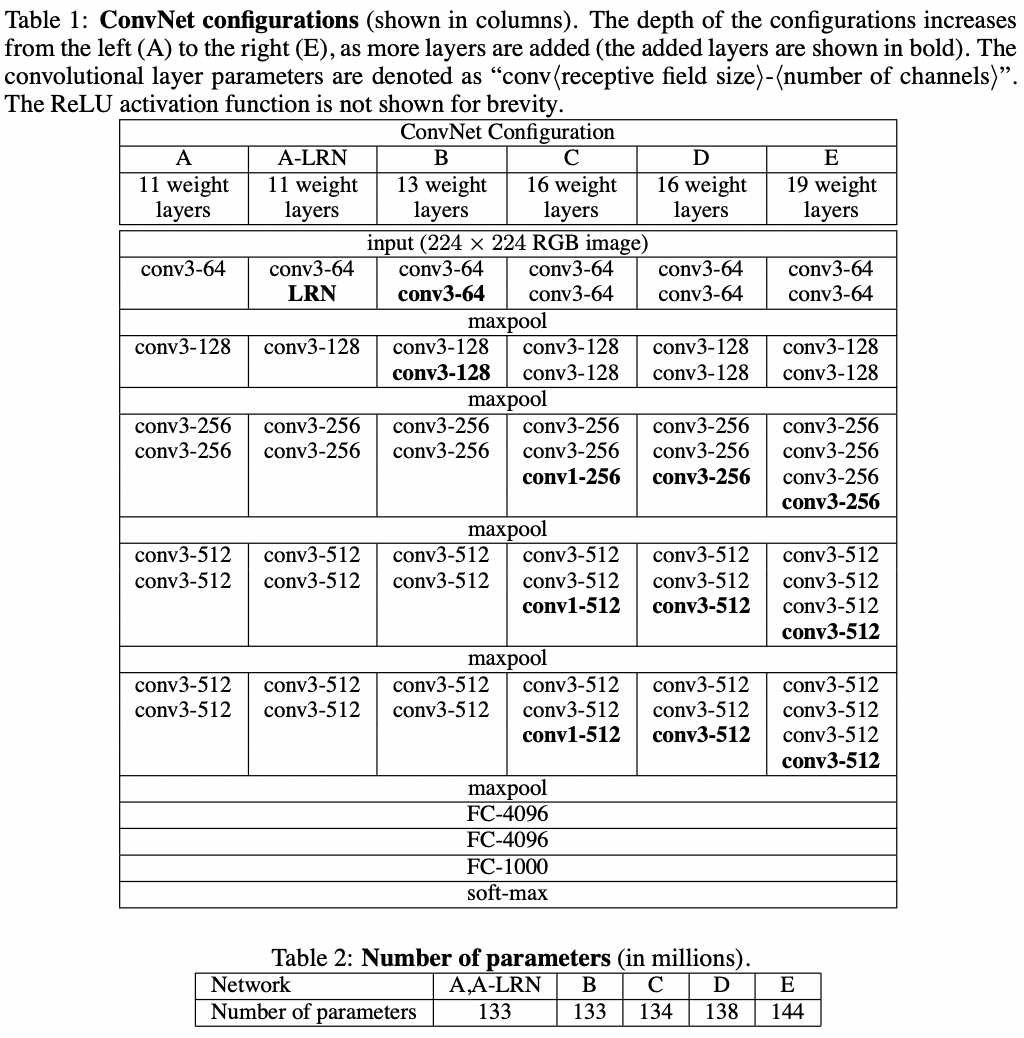
이번 연구에서 평가할 ConvNet configuration들은 Table 1에 요약되어있고 column당 하나의 모델이다.

지금부터는 네트워크의 이름을 A-E사이로 이름을 부르겠다.

모든 configuration들은 2.1에서 설계한 구조를 따르고 서로 깊이만 다르게 한다: 11개의 가중치 층을 갖는 network A부터 19개의 가중치 층을 갖는 network E

합성곱층의 채널 수는 꽤 작다, 64부터 시작해서 512가 될 때까지 2를 곱한다.

Table 2에서는 각 configuration별로 매개변수의 수를 보여준다.

더 깊은 구조임에도 불구하고 가중치의 수는 우리의 network들이 더 깊이가 얕은 network와 비교했을 때 합성곱층의 채널 수도 적고 receptive field도 작아서 가중치가 더 많지 않다.

2.3 Discussion

ConvNet 구성들은 ILSVRC-2012와 ILSVRC-2013에서 입상한 가장 좋은 모델과 꽤 다르게 생겼다.

Krizhevsky의 11x11 크기의 필터를 stride 4만큼 씩 움직이는 합성곱층과 와 Zeiler&Fergus의 7x7 크기의 필터를 stride 2만큼 씩 움직이는 합성곱층처럼 큰 receptive field를 사용하기 보다 우리는 전체 네트워크에서 3x3 크기의 receptive field를 사용하고 stride는 1씩 움직였다.

spatial pooling없이 두개의 3x3 크기의 필터를 사용하는 합성곱층을 사용하는 것은 5x5 크기의 receptive field를 사용하는 합성곱과 같다는 것을 쉽게 알 수 있다 ; 3x3 합성곱이 3개면 7x7 receptive field와 같은 효과를 보인다.

그렇다면 3x3 합성곱을 3개 연달아 사용하는 것이 7x7 합성곱을 1개 사용하는 것과 비교하여 우리가 어떤 이점을 얻는가?

첫째, 하나의 non-linear rectification layer를 사용하는거보다 3개의 non-linear rectification layers를 통합하여 사용하여 decision function을 더 차별적으로 만들 수 있다.

둘째, 매개변수의 수를 줄일 수 있다 : 만약 3개의 3x3 합성곱 stack의 입력과 출력이 C개의 채널을 갖는다면 stack의 매개변수는 $3(3^2C^2)=27C^2$ 개가 될것이다 ; 동시에 하나의 7x7 합성곱층은 $7^2C^2=49C^2$개의 가중치가 필요하다. 이전에 비해 가중치 수가 81% 증가한다.

이는 7x7 합성곱층에 regularization을 부과하여 사이사이 non-linearity가 주입된 3x3 필터들로 분해되도록 하는 것으로 보일 수 있다.

configuration C와 같이 1x1 합성곱층을 포함시키면 receptive field에 영향을 주지 않고 decision function에 non-linearity를 추가할 수 있다.

여기서 1x1 합성곱은 입력과 출력의 채널이 같아지도록 입력을 같은 차원에 선형 투영을 하지만 rectification 함수에 의해 추가된 non-linearity가 도입된다.

1x1 합성곱층은 최근 Lin의 “Network in Network” 구조에 활용되었다는 것을 알아야 한다.

Ciresan에 의해 이전부터 작은 크기의 합성곱 필터가 사용되었지만, 그들의 network들은 우리의 network보다 충분히 얕고 대규모 데이터셋 ILSVRC로 평가해보지 않았다.

Goodfellow가 11개의 가중치층을 갖는 깊은 ConvNet을 거리의 숫자 인식 작업에 적용했더니 깊이가 깊어질수록 더 좋은 성능을 보였다고 한다.

ILSVRC-2014 분류 작업에서 최고 실적을 보인 GoogLeNet은 우리와 따로 개발되었지만, 작은 필터를 이용한 합성곱과 매우 깊은 ConvNet(22 가중치 층)라는 점에서 유사하다. (합성곱 필터는 3x3과 1x1 외에도 5x5를 사용했다.)

그러나 GoogLeNet의 topology는 우리가 설계한 구조보다 복잡하고 feature map의 saptial resolution이 첫 번째 합성곱층에서 계산량을 줄이기 위해 더 공격적으로 줄어든다.

우리의 모델은 GooLeNet보다 single-network classification accuracy 측면에서 뛰어나다.

3. Classification Framework

이전 장에서 우리의 네트워크의 구성을 자세하게 살펴보았다.

이번장에서는 classification ConvNet training과 evaluation을 자세하게 살펴보겠다.

3.1 Training

ConvNet 학습과정은 일반적으로 Krizhevsky를 따라했다.(나중에 설명하지만 학습 이미지의 크기를 키우고 잘라서 만든 샘플은 사용하지 않았다.)

즉, 학습은 multinomial logistic regression을 목적으로 mini-batch gradient descent(LeCun의 역전파를 기반으로)를 momentum과 함께 사용해 optimising 했다.

batch size는 256 momentum은 0.9으로 설정했다.

0.0005값을 weight decay로 설정한 L2 regularization과 dropout ratio를 0.5로 설정하여 첫 두개의 전결합층에 Dropout regularization을 적용했다.

학습률은 0.02로 초기설정을 했고 validation set accuracy가 높아지지 않을 때 10씩 나눠줬다.

전체적으로, 학습률은 3번 감소했고 학습은 370000iteration 뒤에 멈췄다(74epoch).

AlexNet과 비교해 우리 구조가 더 많은 매개변수와 더 깊은 네트워크임에도 더 적은 epoch수로 수렴할 수 있었던 이유는

1. 더 깊지만 작은 합성곱 필터가 주는 암시적 정규화
2. 특정 층의 pre-initialisation

네트워크 가중치의 초기설정은 중요하다, 왜냐하면 안좋은 초기설정은 deep net에서 gradient의 불안정한 성질 때문에 학습을 멈추게 하기 때문이다.

이 문제를 해결하기 위해 random 초기설정으로 학습하기에 충분히 얕은 configuration A부터 학습 시켰다.

그리고나서, 더 깊은 구조를 학습시킬 때, 첫 4개의 합성곱 층과 뒤에 3개의 전결합 층의 가중치를 A의 결과와 똑같이 설정해주고 중간 층은 random initialisation했다.

사전 초기설정된 층의 학습률을 줄이지 않고, 학습하는 동안 변경하도록 했다.

random initialisation의 경우, 가중치들이 평균이 0이고 표준편차가 0.01인 분포를 따르는 표본에서 추출했다.

편향들은 0으로 초기설정했다.

논문 출판 후에 우리는 Glorot&Bengio(Xavier)의 random initialisation procedure를 통해 사전학습 없이 임의 설정된 가중치를 사용하는것이 가능하다는 것을 알았는데 이는 주목할만 하다.

224x224크기의 입력 이미지를 받기 위해서 학습 이미지들의 크기를 조절하고 임의로 잘랐다.(한번 crop하면 한 iteration동안 사용된다.)

학습 데이터를 더 증가시키기 위해서, crop하기 전에 임의로 horizontal flipping과 RGB colour shift를 했다.(AlexNet과 같이)

학습 이미지의 크기 조절은 밑에서 설명한다.

학습 이미지 크기

S를 학습이미지를 isotropically-rescaled 했을 때 짧은 쪽이라고 하자.(S를 training scale이라고도 한다)

자를 크기가 224x224로 고정된 반면, 원칙적으로 S는 224 이상의 값을 받을 수 있다. :

S=224라면 crop은 전체 이미지를 capture한다, 학습 이미지의 짧은 부분을 완전히 사용한다; S»224라면 crop은 작은 객체나 객체의 일부를 포함하는 이미지의 작은 부분일 것이다.

training scale S를 정하기 위해 두가지 접근을 고려한다.

먼저 S를 single-scale training(한개의 값)과 같이 고정하는 것이다.

연구에서, AlexNet과 같이 256의 값으로도 해보고 384로도 고정해 보았다.

주어진 ConvNet 구성에서, 우리는 첫 번째 네트워크를 S=256으로 학습시켰다.

S=384인 네트워크의 학습 속도를 높이기 위해, S=256일때 학습한 가중치로 초기설정을 하고 학습률을 0.001로 초기설정을 했다.

두번째 접근은 S를 multi-scale training(범위 지정)으로 설정하는 것이다. 각 이미지는 개별적으로 S의 범위에서 무작위로 한 값을 정해 크기조절을 진행한다.

S의 범위는 256~512로 정했다.

이미지 안에 객체들이 크기가 다를 수 있기 때문에, 학습 중에 이를 계산하는 것이 좋다.

이것은 하나의 모델이 넓은 범위에 걸쳐 객체를 인식하도록(scale jittering) 학습 데이터를 늘린 것처럼 보일 수 있다.

속도 문제 때문에 S=384인 single-scale model이 사전 학습한 모든 층의 가중치를 fine-tuning해서 같은 configuration인 multi-scale model을 학습 시켰다.

3.2 Testing

test scale Q를 사용해 이미지를 isotropically rescale한다.

Q는 S와 같을 필요는 없다.

그리고나서, 네트워크를 조밀하게 rescale된 test image에 적용한다.

전결합 층들은 먼저 합성곱 층으로 전환된다. 첫번째 FC는 7x7 합성곱으로 두번째 FC는 1x1 합성곱으로 전환.

네트워크의 모든층을 합성곱층으로 만든 네트워크를 uncropped인 전체 이미지에 적용한다.

결과는 입력 이미지의 크기에 따른 variable spatial resolution과 class score map이고 채널의 수는 클래스의 수와 같다.

마지막으로, 이미지의 고정된 크기의 vector of class scores를 얻기 위해, class score map은 공간적 평균을 취한다. (sum-pooled)

또한, test set을 horizontal flipping으로 증가시킨다; 원본과 뒤집은 사진의 soft-max class posteriors를 평균내서 최종 수치를 얻는다.

합성곱 네트워크는 전체 이미지에 적용되기 때문에 test 때 여러개의 자른 sample은 필요없다. 각 crop별로 네트워크가 계산을 다시 하는것은 효율이 적다.

동시에, Szegedy에 의하면 큰 crop 집합을 사용하는 것은 입력 이미지를 미세하게 추출하기 때문에 합성곱 네트워크를 사용하는 것보다 정확도를 향상시킨다고 한다.

또한, multi-crop 평가는 합성곱의 결정 조건이 다르기 때문에 세밀한 평가가 가능하다: ConvNet을 crop에 적용하면, padding을 하지 않는다, 반면 dense evaluation의 경우 같은 crop에 대한 padding은 이미지의 이웃 부분에서 합성곱과 공간 pooling으로 자연스럽게 생긴다, 그래서 실질적으로 전반적인 네트워크의 수용영역이 커지고 많은 context가 capture된다.

multiple crops로 인한 계산 시간 증가는 실제로 정확도를 올리지 못한다고 생각하지만, 추론을 위해 네트워크를 스케일당 50crop(5x5 regular grid with 2flips)을 사용해 평가했다. 이때 Szegedy의 4 스케일에 걸친 144crops에 비교할만한 3스케일에 걸쳐 150crops를 평가함.

3.3 Implementation Details

구현은 C++ Caffe toolbox를 사용했다.

대신 충분히 많은 변경사항을 적용했다.

여러개의 GPU를 하나의 시스템에 설치하여 학습과 평가를 수행하고 학습과 평가는 자르지 않은 전체 사이즈의 이미지를 여러개의 크기인 상태로 진행했다.

다중 GPU 학습은 데이터의 수평성을 이용하여 각 학습 이미지의 batch를 몇개의 GPU batch로 나누어 수행했다.

GPU batch gradient가 계산되고 난 뒤, 그들 전체 batch의 gradient를 얻기 위해 평균 계산을 했다.

Gradient계산은 GPU들 사이에서 동시에 일어나서 결과는 한개의 GPU를 사용한 경우와 같게 나온다.

ConvNet의 학습 속도를 높이는 많은 정교한 방법들이 제안되었지만(네트워크에서 다른 계층에 모델과 데이터의 병렬 처리), 개념적으로 더 간단한 내용인 우리 네트워크가 한개의 GPU보다 4개의 GPU로 학습해서 3.75배의 속도 향상을 시켰다.

4개의 NVIDIA Titan Black GPU를 장착한 시스템에서 하나의 네트워크를 학습 시키는 경우 구조에 따라 2-3주가 걸렸다.

4. Classification Experiments

Dataset

4장에서는 이미지 분류 결과 얻기 위해 ILSVRC 2012-2014에 사용된 데이터를 사용했다.

데이터에는 1000개의 클래스가 있고 130만개의 학습 데이터셋과 validation을 위한 5만개 그리고 평가를 위한 10만개로 나눴다.

분류 성능 평가는 top-1과 top-5를 통해 이루어졌다.

top-1은 잘못 분류된 이미지의 비율을 구하고; top-5는 ILSVRC에서 주로 사용하는 평가 기준으로 예측한 5개의 범주에 실제 class가 있는 비율을 계산한다.

대부분의 실험을 위해, validation set을 test set으로 사용했다.

특정 실험들은 test set을 사용했고 ILSVRC-2014에 “VGG”팀으로 입상하여 ILSVRC서버에 공식적으로 제출됐다.

4.1 Single Scale Evaluation

각 모델을 single scale로 성능을 평가한다.

test 이미지의 크기는 $Q=S=0.5(S_{min}+S_{max})$로 설정했다.

먼저, local response normalisation은 normalisation층이 없는 모델 A를 향상시키지 못했기 때문에 다른 더 깊은 구조에도 normalisation을 적용하지 않았다.

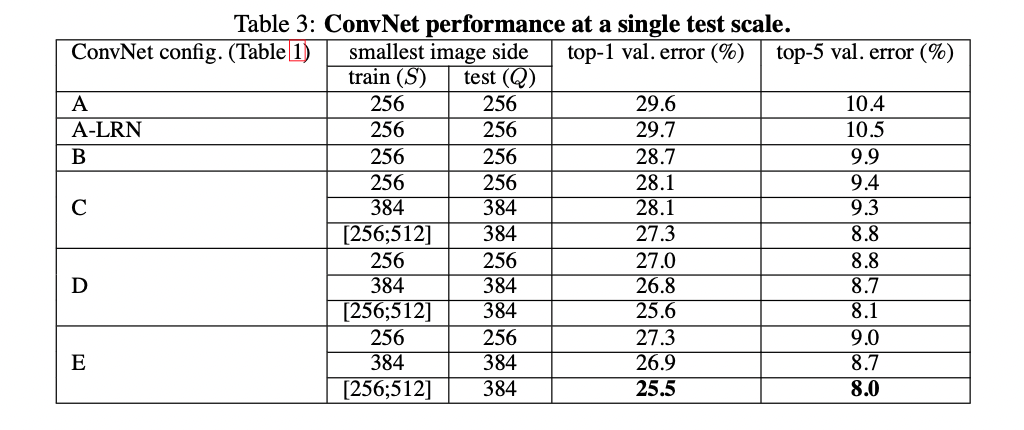
다음으로, ConvNet이 깊어질수록 classification error가 감소하는 것을 관찰했다 : A의 11층부터 E의 19층까지 실험했다.

같은 깊이임에도, C(1x1 conv)가 D(3x3 conv)보다 성능이 안좋았다.

C>B : 추가적인 non-linearity가 도움이 된다

D>C : trivial 하지않은(1보다 크기가 큰)합성곱 필터를 사용해 capture spatial context하는 것도 중요하다.

error rate는 모델의 깊이가 19층일 때 포화 되었지만 더 깊은 모델은 더 큰 데이터셋에서 효과적일지 모른다.

또한 B와 B의 3x3 필터를 쓰는 합성곱층의 쌍을 5x5 필터를 쓰는 합성곱으로 대체한 네트워크와 비교를 해보았다.

얕아진 네트워크의 top-1 error가 B보다 7% 높아진것으로 보아 깊고 작은 필터를 사용한 네트워크가 얕고 큰 필터를 사용한 네트워크보다 뛰어나다는 것을 확인했다.

마지막으로, 학습할 때 $S\in[256;512]$에서 scale jittering 하게 되면 test time에서 single scale을 사용하더라도 S가 256이나 384로 고정된 값을 갖는 것 보다 상당히 더 좋은 결과를 보인다.

따라서 training set augmentation by scale jittering은 capturing multi-scale image statistics에 도움을 준다는 것을 알 수 있다.

4.2 Multi-Scale Evaluation

ConvNet 모델을 single scale로 평가한 후, scale jittering이 test time에 미치는 영향을 평가해보겠다.

이것은 모델을 Q를 다른값들로 바꿔보는 것과 같이 test image를 여러 크기의 버전으로 모델을 실행시킨다, 그 다음에 결과 클래스의 posterior에 대해 평균을 계산한다.

training고 testing scale의 차이가 성능저하를 일으킨다는 점을 고려하여 고정된 S로 학습한 모델들을 S와 비슷한 3개의 Q로 평가 했다 : $Q=\left{S-32,\ S,\ S+32\right}$

동시에, 학습 때 scale jittering은 네트워크가 test time에서 광범위한 크기에 적용되도록 하기 때문에 모델은 $S\in\left[S_{min};S_{max}\right]$인 다양성으로 학습하고 $Q=\left{S_{min},\ 0.5(S_{min}+S_{max}),\ S_{max}\right}$ 로 더 큰 범위에 걸쳐 평가했다.

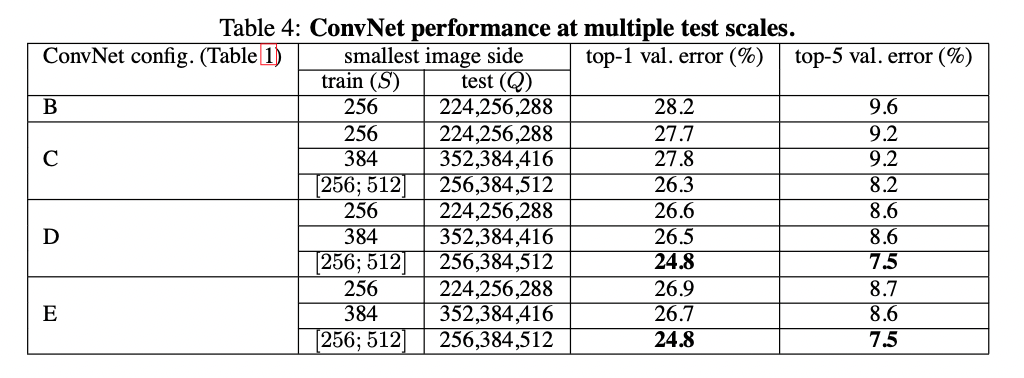
결과를 보면 test time에서 scale jittering은 더 좋은 성능으로 이끈다(같은 모델을 single scale에서 평가한것과 비교하여).

이전처럼, 더 깊은 네트워크(D and E)가 최고의 성능을 보여주고 scale jittering으로 학습한 것은 고정된 S로 학습한 모델보다 더 좋다.

가장 좋은 네트워크 성능은 validation에서 top-1 : 24.8% / top-5 : 7.5%이다.

test set에서 E 네트워크의 top-5 error는 7.3%가 나왔다.

4.3 Multi-Crop Evaluation

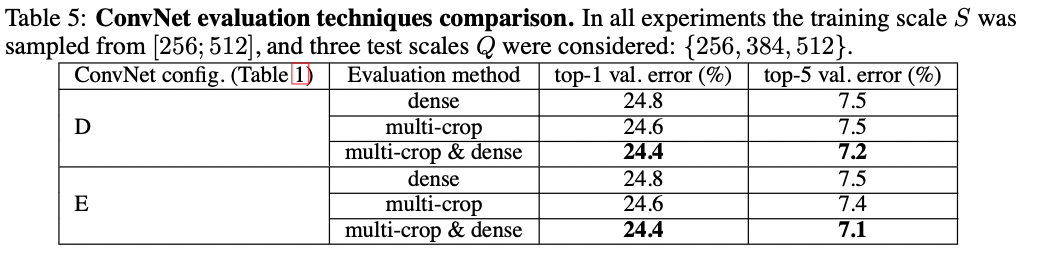
dense ConvNet evaluation과 mult-crop evaluation을 비교했다.

또한, 이 둘의 soft-max 결과를 평균내어 두가지 방법을 보완한 방법도 평가했다.

보이는 바와 같이 multiple crops를 사용해 평가하게 되면 dense evaluation보다 더 좋은 결과가 나오고 두가지를 조합해서 사용하면 더 좋은 결과가 나온다.

위에서 말했듯이 이것은 합성곱 결정 조건이 다르게 나타나기 때문이다.

4.4 ConvNet Fusion

지금까지, 각 ConvNet별로 성능을 평가했다.

이번에는 몇가지 모델의 soft-max class posteriors를 평균내어 결과를 조합해보겠다.

이 과정은 모델들을 보완해주기 때문에 성능을 개선시키고 ILSVRC-2012에서 Krizhevsky가 사용했었고 2013에는 Zeiler&Fergus가 사용했다.

ILSVRC 제출 당시 우리는 single-scale 네트워크와 multi-scale model D(전결합 층만 미세조정을 한)만 학습 시켰다.

7개의 네트워크를 조합한 결과 ILSVRC test error는 7.3%였다.

그 뒤, multi-scale 모델중 최고 성능을 보이는 D와 E만 조합했더니 test error는 dense evaluation에서 7.0%이고 dense와 multi-crop을 합쳐서 평가하니 6.8%였다.

참고로 가장 좋은 single model 은 7.1%의 error를 보였다.

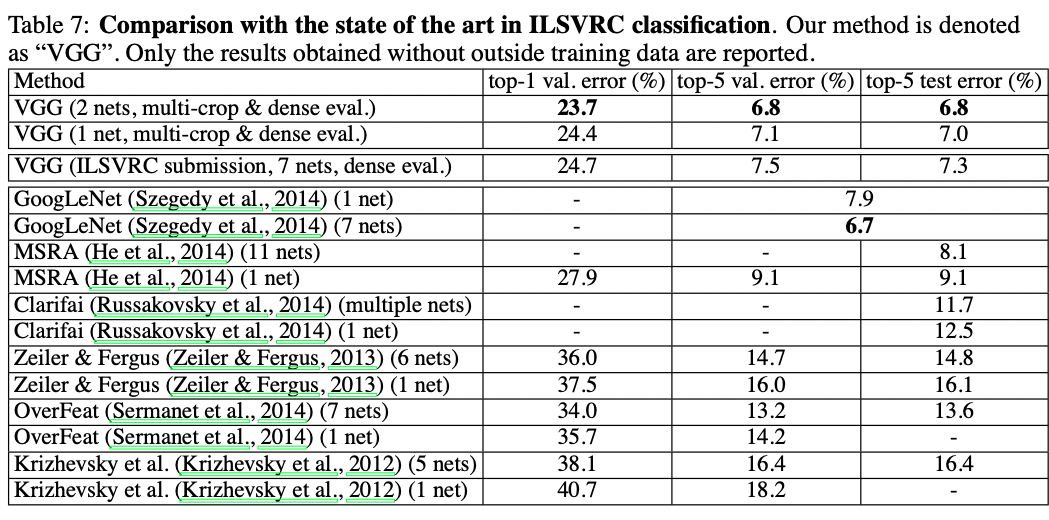
4.5 Comparison with the State-of-the-art

마지막으로, 우리의 결과를 최신 기술과 비교해 보겠다.

ILSVRC-2014때 분류작업에서, VGG팀은 7개의 모델을 조합해서 7.3%의 test error를 나타내며 2등을 차지했다.

그 뒤, 우리는 D&E의 조합으로 error를 6.8까지 낮췄다.

결과에서 보이듯 이전 세대(ILSVRC-2012,2013)의 최고 모델과 비교해 상당히 좋은 결과를 우리 very deep ConvNet이 달성했다.

우리의 결과는 분류작업 우승자인 GoogLeNet(6.7%)과 비교할 수 있을정도이고 실제로 ILSVRC-2013의 우승자 Clarifai(외부 학습 데이터로 11.2% 외부학습 데이터 없이 11.7%)를 능가했다.

ILSVRC에 제출된 대부분의 모델들보다 상당히 적은 양인 2개의 모델을 조합해서 얻은 최고의 결과라는 점에서 매우 놀랍다.

single-net performance를 보면, 우리의 구조가 최고의 결과를 달성한다(test error 7.0%), single GoogLeNet를 0.9% 능가하는 수치다.

참고로, 우리는 LeCun의 구조에서 많이 벗어나지 않고 실질적으로 깊이만 증가시켰다.

5. Conclusion

이번 연구에서 우리는 매우 깊은 신경망(최대 19의 가중치 층)을 대규모 이미지 분류를 통해 평가했다.

이것으로 표현깊이는 분류 정확도에 이점이 된다는 것과 ImageNet challenge dataset에서 최첨단 모델의 성능은 ConvNet구조의 실질적 깊이를 깊게 함으로써 얻을 수 있다는 것을 확인했다.

부록에서, 우리는 또한 우리의 모델이 광범위한 작업과 data set으로 잘 일반화되어 덜 깊은 구조로 구축된 더 복잡한 인식 파이프라인과 성능이 같거나 능가한다는 것을 보였다.

이 결과로 visual representation에서 depth의 중요성을 다시한번 확인했다.