AlexNet
AlexNet
ImageNet Classification with Deep Convolutional Neural Networks
1. Introduction
최근 객체 인식은 기계학습 방법을 필수적으로 동반한다.
성능 개선을 위해 데이터를 더많이 모으고, 강력한 모델을 학습 시키고, 그리고 overfitting을 방지하기 위해 더 좋은 기술을 사용한다.
최근까지, 라벨된 이미지데이터는 수만개로 비교적 적은 양이었다.
이정도 양의 데이터 집합이라도 label-preserving transformation으로 증가된 상태라면 간단한 인식 문제가 꽤 잘 해결된다.
예를 들어 최근 숫자 인식에 대한 error rate는 인간의 성능과 비슷하다.
하지만 실제의 객체는 상당한 다양성을 보이기 때문에, 그들을 학습하기 위해서는 더 많은 학습 데이터가 필요하다.
사실, 작은 양의 데이터 셋의 단점은 널리 알려져있었지만, 이 문제에 대한 해결은 수백만개의 라벨링된 이미지 데이터셋을 최근(2012)에야 준비할 수 있었기 때문에 해결이 되었다.
새로운 큰 데이터셋에는 LabelMe와 ImageNet이 있다.
수백만 이미지를 통해 수천개의 객체를 학습하려면, large learning capacity인 모델이 필요하다.
그러나, 거대한 객체인식 작업의 복잡성은 ImageNet만틈 큰 데이터의 양으로도 해결할 수 없다, 그래서 모델이 가지고 있지 않은 데이터에 대해 올바른 loss값을 도출하기 위해서는 prior knowledge가 필요하다.
CNN의 capacity는 깊이와 크기를 다양하게 하여 조절할 수 있고 그들은 강력하고 대부분 정확한 가정들(고정적인 통계량과 지역적 픽셀 종속성)을 만들어낸다.
그러므로, 비슷한 크기의 층을 가진 표준 feedforward 신경망과 CNN을 비교하면 CNN의 이론적 최고의 성과는 약간 더 안좋은 반면 CNN은 더 적은 연결수와 매개변수의 수를 가지기 때문에 학습하기 더 쉽다.
CNN의 매력적인 성능과 local구조의 효율에도, 그들은 여전히 대규모 고해상도 이미지에 적용하기에는 비용적으로 매우 비싸다.
운좋게도, 2D 합성곱에 매우 최적화된 최근의(2012)GPU들은 매우 큰 CNN을 학습 시키기에 충분하고, ImageNet 같은 최근 데이터들은 과적합 없이 모델을 학습 시키기 위해서 충분한 학습 샘플을 가지고 있다.
이 논문의 주요 내용은 다음과 같다 : 지금까지(2012) 가장 큰 CNN중 하나를 ILSVRC2010과 2012에 사용된 ImageNet의 부분을 학습시키고 이 데이터에 대해 지금까지 보고된 내용중 최고의 결과를 얻었다.
2D 합성곱에 최적화된 GPU와 CNN을 학습 시키는 법을 기술했다.
성능을 개선하고 학습 시간을 줄이는 새롭고 평범하지 않은 feature들을 많이 사용한다.
이 네트워크의 크기는 120만개의 데이터 수로도 과적합을 일으키기 때문에, 과적합을 막기 위해 효과적인 방법을 사용했다.
5개의 합성곱층과 3개의 전결합층을 포함하고, 이 depth는 중요해 보인다 : 어떤 층을 빼는것이 성능 저하를 일으킨다는 것을 확인했다.
2. The Dataset
ImageNet은 22000개의 범주를 가지는 1500만개의 labeled high-resolution image를 가지고 있다.
이미지들은 웹과 Amazon’s Mechanical Turk crowd-sourcing tool을 통해 사람이 직접 라벨링 했따.
2010부터, Pascal Visual Object Challenge 중 하나인 ILSVRC가 열렸다. ILSVRC는 ImageNet의 부분인 1000개의 각 범주가 1000개 정도의 이미지를 가지는 데이터를 사용한다.
전체적으로, 120만개의 학습 이미지, 5만개의 validation 이미지와 15만개의 test 이미지로 구성된다.
ILSVRC-2010은 ILSVRC 중에서 test set label들을 사용할 수 있는 유일한 버전이기 때문에, 이번 실험에서 대부분 이 버전을 사용했다.
ILSVRC-2012에 참가했기 때문에 test set label은 사용할 수 없지만 이 버전에 대해서도 성능 결과를 볼것이다.
ImageNet은 관습적으로 두가지 error rate를 계산한다. top-1과 top-5 error rate이다.
우리 시스템은 입력차원이 정해져있지만, ImageNet은 다양한 해상도의 이미지로 구성된다.
그러므로, 우리는 이미지들을 256x256 크기의 해상도로 전처리 한다.
직사각형 이미지가 주어진다면, 짧은 길이를 256으로 rescale하고 중심에 위치한 256x256 크기만큼 자를 것이다.
각 픽셀에 평균값을 빼는것을 제외하고 이미지에 다른 전처리는 안했다.
그래수 우리의 network는 RGB이미지의 중심을 학습했다.
3. The Architecture
구조는 8개의 학습층으로 5개의 합성곱층과 3개의 전결합 층으로 구성된다.
이제 네트워크 구조에서 사용된 새롭고 평범하지 않은 feature에 대해 설명한다.
제일 중요한것부터 순서대로 설명하겠다.
3.1 ReLu Nonlinearity
모델이 사용하는 표준적인 뉴런의 결과 함수는 tanh와 sigmoid이다.
경사하강법에서 학습 시간동안, 이러한 saturating nonlinearities들은 non-saturating nonlinearities보다 속도가 더 느려진다.
Nair와 Hinton에 따라 우리는 Rectified Linear Units(ReLUs)를 통해 non-saturating nonlinearities를 사용한다.
\[f \mathsf{\ \ is\ \ non-saturating}\\ \mathsf{iff}\ \ (|\lim_{z\rightarrow-\infty}f(z)|=+\infty)\lor(|\lim_{z\rightarrow+\infty}f(z)|=+\infty)\\ \mathsf{others,\ }f\mathsf{\ is\ saturating}\]tanh와 비교해 ReLU를 사용한 Deep CNN은 몇배 더 빠르게 학습한다.
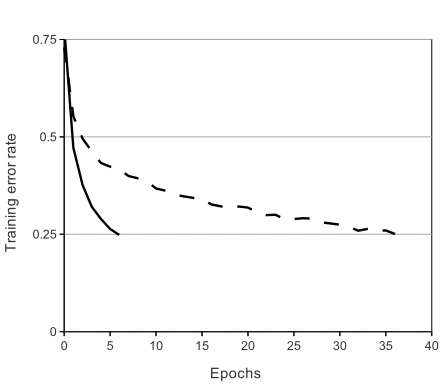
A four-layer CNN with ReLUs(solid line) 가 CIFAR-10을 사용했을 때 학습에러 25%에 도달하기 까지 걸리는 시간은 tanh(dashed line)를 사용할 때보다 6배 빠르다.
위 결과에서 보이는 것과 같이, 이번 실험에서 큰 신경망에 기존에 사용하던 saturating neuron model을 사용했다면 실험을 할 수 없었을 것이다.
우리가 전통적인 neuron model을 바꾸려고 생각한 첫번째가 아니다.
적용할 데이터에 맞게 neuron model을 바꾼 사람들이 많았다.
하지만, 이 데이터셋에서 과적합을 방지를 최 우선으로 여겨서, 그들이 관찰한 가속화 능력은 ReLUs를 사용한 이 보고서와 맞지 않는다.
빠른 학습은 큰 데이터를 학습하는 큰 모델의 성능에 중요한 영향을 미친다.
3.2 Training on Multiple GPUs
GTX 580 GPU 한개는 3GB 메모리만 사용할 수 있고 이 메모리량은 네트워크의 최대 학습량을 제한한다.
120만개의 학습 샘플들은 하나의 GPU에서 학습하기에 너무 크다.
따라서, GPU를 2개를 사용한다. 최근(2012) GPU는 주메모리에 접근하지 않고 서로 직접 읽고 쓰는 능력이 있기 때문에 병렬연결 처리가 잘된다.
parallelization scheme은 뉴런의 절반을 각 GPU에 담는 것이다.(단, GPU간의 통신은 특정 층에서만 이루어진다.)
패턴의 연결을 고르는 것은 cross-validation에서 문제가 되지만, 이런 연결 방식은 계산량을 해결 가능한 수준이 되도록 튜닝하는것이 가능하게 한다.
이 구조는 column들이 종속적이라는것을 빼면Ciresan의 “columnar” CNN과 약간 비슷하다.
이 내용은 kernel을 반으로 줄인 네트워크를 하나의 GPU로 학습한 것과 비교하여 top-1과 top-5 error rate를 1.7%와 1.2%씩 낮춘다.
두 개의 GPU는 학습 시간이 하나일 때보다 약간 빠르다.
3.3 Local Response Normalization
ReLUs는 뉴런의 saturating을 막기위해 입력을 normalization하지 않아도 된다는 좋은 특성이 있다.
만약 어떤 학습 샘플이 양의 입력을 ReLU에 제공한다면, 학습은 해당 뉴런에서 진행될 것이다.
그러나, 우리는 local normalization이 generalization을 돕는다고 여긴다.
response-normalized는 다음과 같이 계산한다.
\[b^i_{x,y}={a^i_{x,y}\over \left(k+\alpha\sum\limits^{\min(N-1,i+n/2)}_{j=\max(0,i-n/2)}(a^j_{x,y})^2\right)^\beta}\]kernel의 순서는 학습 전에 임의로 배정된다.
이런 reponse normalization은 실제 뉴런에서 영감을 받아 만들어져 다른 커널을 사용해서 얻은 뉴런 출력값들 중 큰 활성값들 사이에 경쟁을 만드는 lateral inhibition 기능을 한다.
$k,n,\alpha,\beta$ 는 validation set을 통해 결정되는 하이퍼파라미터들이다; 실험적으로
$k=2,n=5,\alpha=10^{-4},\beta=0.75$ 를 사용했다.
이 normalization을 ReLU를 적용한 이후에 적용했다.
이 내용은 local contrast normalization내용과 유사함을 보이지만, response-normalized는 평균값을 빼지 않아 “brightness normalization”이라 명명된다.
Response normalization은 top-1과 top-5 error rate를 각각 1.4%와 1.2%씩 낮춘다.
또한, CIFAR-10에 효과적인것을 확인했다 : 4개의 CNN에 normalization을 적용하면 11%의 test error가 나오고 without normalization인 경우는 13%의 test error가 나온다.
3.4 Overlapping Pooling
CNN에서 Pooling layer는 같은 kernel map에서 이웃한 뉴런 그룹들의 결과를 요약해준다.
전통적으로, 인접한 pooling unit들로 인해 요약된 neighborhood 들은 overlap되지 않는다.
더 정확하게는 pooling unit 하나당 pooling layer는 zxz 크기의 neighborhood를 요약하는데 이 pooling unit이 grid의 형태로 가로와 세로가 각각 s 간격만큼 움직이는 층을 pooling layer라고 한다.
만약 s와 z를 같은 값으로 설정한다면, 우리는 CNN에서 옛날부터 쓰이는 전통적인 local pooling layer를 얻게 된다.
s<z인 경우에는 overlapping pooling을 한다.
이 overlapping pooling이 우리 network에 $s=2,z=3$의 형태로 쓰인다.
이 내용은 top-1과 top-5 error rate를 각각 0.4%와 0.3%씩 줄인다. ($s=2,z=2$로 설정한 non overlapping pooling과 비교하여)
일반적으로 overlapping pooling을 사용하면 과적합이 좀 덜 일어나게 되는걸 관찰했다.
3.5 Overall Architecture
전반적인 구조는 5개의 합성곱층과 3개의 전결합층으로
총 8개의 가중치를 갖는 층으로 이루어져있다.
마지막 전결합층의 결과는 1000-way softmax에 입력된다.
우리 network는 multinomial logistic regression을 최대화하는데 이것은 예측 결과에서 맞게 labeling한 log-probability를 모든 학습 case값들의 평균을 극대화하는 것과 같다.
2,4, 그리고 5번째 합성곱층은 같은 GPU에 속하는 이전층의 kernel map들과만 연결되어있다.
3번째 합성곱층의 kernel들은 2번째 층의 모든 kernel map들과 연결했다.
Response-normalization layer들은 첫번째와 두번째 합성곱층 뒤에 적용한다.
Max-pooling layer들은 두 response-normalization 층 뒤와 5번째 합성곱층 뒤에 위치시킨다.
ReLU non-linearity는 모든 합성곱층과 전결합층 뒤에 적용한다.
C1
227x227x3 — (96, 11, 11, 3), p=0, s=4 → 96x55x55
S2
96x55x55 —(3, 3), p=0, s=2 →96x27x27
C3
96x27x27 —(256, 5, 5, 96), p=2, s=1 → 256x27x27
S4
256x27x27 —(3,3), p=0, s=2 →256x13x13
C5
256x13x13 —(384, 3, 3, 256), p=1, s=1 →384x13x13
C6
384x13x13 —(384, 3, 3, 384), p=1, s=1 →384x13x13
C7
384x13x13 —(256, 3, 3, 384), p=1, s=1 →256x13x13
S8
256x13x13 —(3x3), p=0, s=2 → 256x6x6
Flatten : 256x6x6 = 9216
FC8
9216 → 4096
FC9
4096 → 4096
SOFTMAX10
4096 → 1000
4 Reducing Overfitting
6000만개의 매개변수가 있다. (60Mb)
1000개의 class를 갖는 ILSVRC가 각 샘플에 이미지를 라벨링할 때 10bits로 제약을 준다 하더라도 과적합 없이 이 많은 매개변수를 학습시키기에는 공간이 부족하다. labeling에만 75Mb
이제 과적합을 없애기 위한 두가지 주요 방법을 말하겠다.
4.1 Data Augmentation
가장 쉽고 일반적으로 데이터를 통해 과적합을 줄이는 방법은 인공적으로 데이터를 label-preserving transformation을 통해 확대하는 것이다.
원본 이미지에 계산을 조금 적용해서 변형을 주기 때문에 디스크에 결과를 저장할 필요는 없다.
GPU로 학습을 하는 동안 CPU로 data augmentation을 하기 때문에 실질적으로 computationally free하다.
첫번째 data augmentation은 translation과 horizontal reflection이다. 256x256 크기의 이미지에서 227x227을 임의로 추출하여 reflection 한다.
이것은 데이터 샘플의 크기를 키워주고 데이터 샘플들은 interdependent해진다.
이런 과정없다면, 이 네트워크는 과적합을 일으켜 우리가 더 작은 네트워크를 사용하게 한다.
test 할 때에는, 227x227를 5장을 추출한다(4개의 코너와 중앙). 그리고 그것의 horizontal reflection까지 총 10장에 대해 예측을 하고 10개의 예측값의 평균을 구한다.
두번째 data augmentation은 학습 이미지에서 RGB채널들의 밝기값을 변경하는 것이다.
특히, 학습 이미지의 RGB픽셀값 집합에 PCA를 진행한다.
각 이미지에, eigenvalue에 비례하는 크기를 평균이 0이고 표준편차가 0.1인 가우시안 분포에서 random variable을 선택하여 곱하고 그렇게 만든 여러 주성분을 더한다.
그러므로 각 RGB 이미지 픽셀의 값이 변하게 된다.
\[\begin{align*} I_{xy}&=\left[I^R_{xy},I^G_{xy},I^B_{xy}\right]^T\\ I'_{xy}&=\left[\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3\right]\left[\alpha_1\lambda_1,\alpha_2\lambda_2,\alpha_3\lambda_3\right]^T \end{align*}\]$\mathbf{p}_i, \lambda_i$ 는 i번째 eigenvector와 eigenvalue이다.
$\alpha_i$ 는 위에 말했던 random variable이고 한 이미지가 다시 학습되기 위해 들어올때까지 그 값을 유지한다. 이미지가 다시 학습되기 위해 입력되면 그 값이 다시 설정된다.
이 내용은 원본 이미지의 중요한 특성을 잡아낸다.
그 특성은 밝기값과 조명값에 대해 불변성을 가진다.
이 내용은 top-1과 top-5 error rate를 1% 줄인다.
4.2 Dropout
여러 종류의 모델들의 예측을 조합하는 것은 test error를 줄이는 매우 성공적인 방법이지만 큰 신경망의 학습 시간에 대한 비용이 매우 크다.
그러나 모델을 조합하는 매우 효율적인 방법이 있다.
“dropout”은 최근(2012) 소개된 기술로 각 은닉 뉴런의 결과를 0.5의 확률로 0의 값을 출력하는 것이다.
“dropped out”된 뉴런들은 forward pass와 back-propagation 진행시 참여하지 않는다.
그래서 입력을 표현할 때마다 신경망은 다른 architecture를 사용하고 모든 architecture들은 가중치를 공유한다.
이렇게 하면 뉴런이 다른 뉴런의 존재에 의존하지 않게 되므로 뉴런의 complex co-adaptation을 줄인다.
그러므로 다양한 뉴런들의 부분집합들과의 결합은 model이robust한 feature를 학습하게 한다.
test에서 우리는 모든 뉴런을 사용하지만 출력에 0.5를 곱하며, 이는 기하급수적으로 많은 dropout network에 의해 생성된 예측 분포의 기하학적 평균을 취하는 데 합리적인 근사치이다.
첫 두 전결합층에서 dropout을 사용한다. dropout을 사용하지 않으면, 우리 네트워크는 상당한 과적합을 보일 것이다.
Dropout은 수렴에 필요한 반복수를 거의 두배로 만든다.
5. Details of learning
모델 최적화에는 SGD를 사용하고 batch size 는 128이다 momentum은 0.9로 하고 weight decay는 0.0005로 설정 했다.
모델이 학습하기 위해 weight decay가 중요하다는 것을 발견했다.
다시말해, weight decay는 단지 regularizer가 아니라 model의 학습 error를 줄여준다는 것이다.
가중치 update 방식은 아래와 같다.
\[\begin{align*} v_{i+1}&:=0.9\cdot v_i-0.0005\cdot\epsilon\cdot w_i-\epsilon\cdot\left\langle{\partial L\over\partial w}|_{w_i}\right\rangle_{D_i}\\ w_{i+1}&:=w_i+v_{i+1} \end{align*}\]각 층의 가중치를 평균이 0이고 표준편차가 0.01인 가우시안 분포를 따르도록 초기설정 했다.
2,4,5 번째 합성곱층과 전결합 층들의 편향을 1로 설정했다.
그리고 나머지 층의 편향은 0이다.
이런 초기 설정은 ReLUs에 양의 입력을 제공함으로써 학습의 초기 단계를 가속화 한다.
모든 층에 동일한 학습률을 적용했다. 이 학습률은 학습동안 수동으로 조정했다.
heuristic은 validation error가 개선되지 않는 경우 현재 학습률을 10으로 나눠서 적용한 것이다.
학습률은 0.01로 초기설정을 했고 종료되기 전에 3번 줄었다.
120만개의 학습 데이터를 90 epochs로 학습했더니 NVIDIA GTX 580 3GB GPU두개로 5~6일이 걸렸다.
6. Results
6.1 Qualitative Evalutaions

제한된 연결성을 가지는 구조로 인해 GPU1에 있는 kernel 들은 color-agnostic(색상에 구애받지 않는)하고
GPU2에 있는 kernel 들은 color-specific하다.
이 특징은 매 학습마다 발견되고 가중치 초기화와 관련이 없다.

사진에서 객체가 중심에 없더라도 사진에서 mite처럼 network에 의해 검출이 될 수 있다.
대부분의 top-5 label들은 합리적이다.
예를들어, 레오파드의 top-5 label들은 고양이과의 다른 종류들이다.
grille과 cherry같은 경우는 사진에서 의도된 초점에 대한 진정한 모호함이 있다.

네트워크의 visual knowledge를 살피는 다른 방법은 마지막 4096차원의 은닉층으로부터 유도된 feature activation을 생각하는 것이다.
만약 작은 Euclidean separation인 두개의 이미지가 feature activation vector에 입력되면, 높은 수준의 신경망이 이 사진들을 비슷하다고 여긴다고 말할 수 있다.
위 사진의 첫번째 column은 test set에서 고른 5개의 사진인고 row는 그 test 사진들을 query image로해서 Euclidean separation이 작은 이미지들을 training set에서 고른 것이다.
pixel 수준에서 선택된 training set의 사진들은 일반적으로 qeury image와 Euclidean separation이 L2만큼 가깝지 않다.
예를 들어 강아지와 코끼리를 보면 그들은 다양한 자세를 보이는것을 알 수 있다.
4096차원인 두 은닉층 사이의 Euclidean distance 계산할 때 실수값을 가지는 vector들은 비효율적이지만 이러한 vector를 짧은 binary 코드로 압축하도록 auto-encoder를 학습시킴으로써 이를 효율적으로 만들 수 있다.
이미지 label을 사용하지 않아서 의미상 같은 이미지이던 아니던 비슷한 edge 패턴을 가진 이미지를 도출하는 이 방법은 auto-encoder를 raw pixel에 적용해 이미지를 도출하는 방법보다 더 좋다.
7. Discusstion
크고 깊은 합성곱 신경망은 매우 도전적인 데이터셋을 supervised learning 했을 때 좋은 결과를 보인다.
우리의 네트워크는 합성곱층을 하나 빼더라도 성능이 저하된다는 것을 알았다.
예를들어, 중간에 어느 층을 제거하는 것은 top-1 성능에 2% 저하를 가져온다.
따라서 깊이는 우리 결과를 만드는데 매우 중요하다.
실험을 단순화하기 위해, 특히 라벨이 붙은 데이터의 양을 크게 늘리지 않고 네트워크의 크기를 크게 늘리기에 충분한 계산 능력이 있는 경우에 도움이 될 것으로 예상되더라도 unsupervised 사전 훈련을 사용하지 않았습니다.
지금까지, 우리는 네트워크의 크기를 키우거나 더 오래 학습시키면 성능이 향상되는것을 알고있지만 인간의 시각 시스템 방법인 아래관자피질(Inferior temporal cortex,IT-cortex 또는 IT)과 대응 되려면 아직 해야하는 일들이 많다.
궁극적으로 우리는 정적인 이미지에서 누락된 부분이나 덜 명백한 매우 유용한 정보를 제공하는 시간적 구조인 video sequences에 크고 깊은 합성곱 네트워크를 사용하고 싶다.