Ch5 오차역전파법
Ch5 오차역전파법
수치 미분을 통해 기울기를 구하는 방법은
구현이 쉽다는 장접이 있지만 시간이 오래 걸린다는 단점도 있다.
오차역전파법을 사용해 효율적으로 계산하겠다.
5.1 계산 그래프
5.1.1 계산 그래프로 풀다.
흐름
- 계산 그래프를 구성한다.
- 그래프에서 계산을 왼쪾에서 오른쪽으로 진행한다. (순전파$\mathsf{^{forward\ propagation}}$)
5.1.2 국소적 계산
계산 그래프의 특징은 ‘국소적 계산’을 전파하여 최종 결과를 얻는다.
따라서 전체 계산이 복잡하더라도 각 단계에서 하는 일은 해당 노드의 ‘국소적 계산’이기 때문에
계산이 간단하지만 그것들이 모여 복잡한 계산을 해낸다.
5.1.3 왜 계산 그래프?
- 국소적 계산을 통해 문제를 단순화할 수 있다.
- 중간 계산 결과를 모두 보관할 수 있다.
- 역전파( back propagation )를 통해 ‘미분’을 효율적으로 계산할 수 있다.
5.2 연쇄법칙
5.2.1 계산 그래프의 역전파
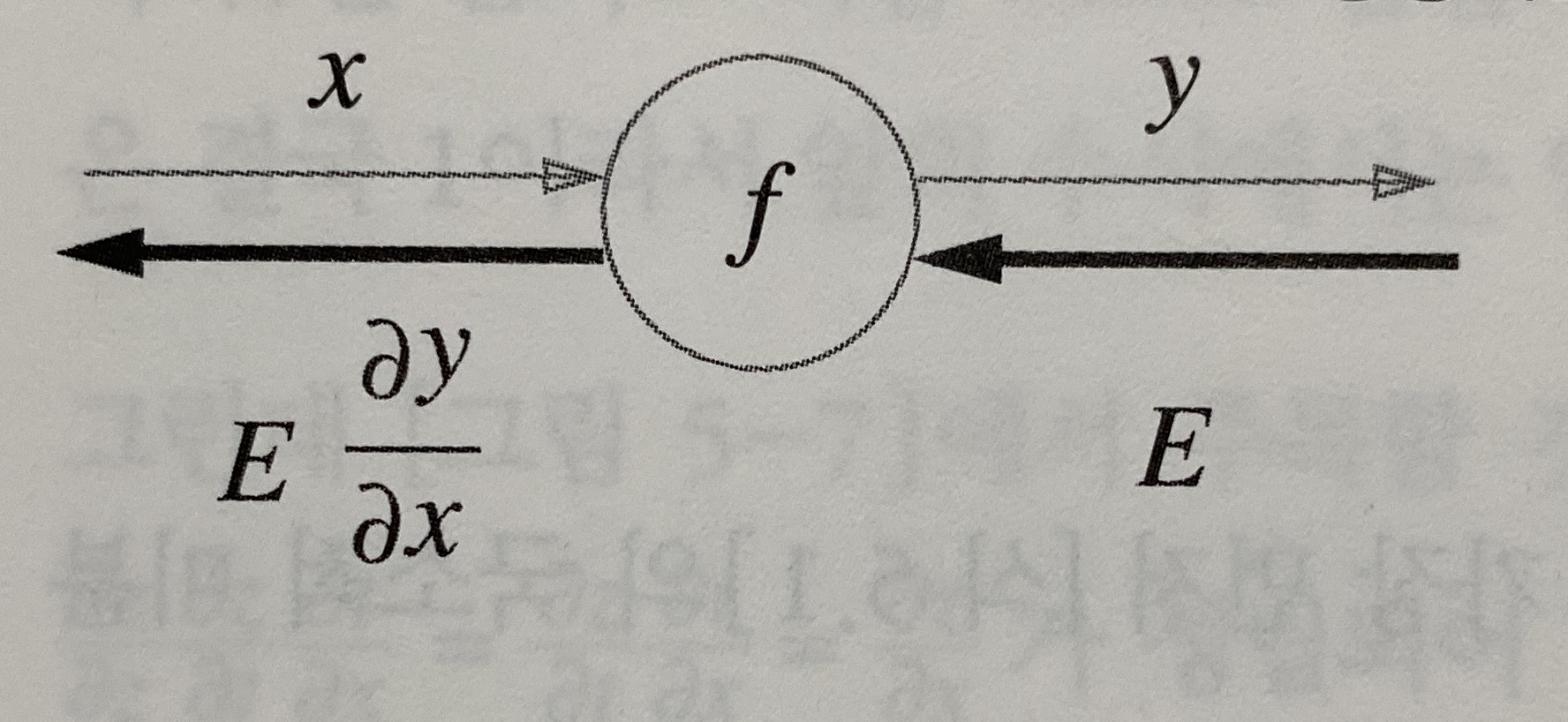
신호 E에 노드의 국소적 미분 $\partial y\over \partial x$를 곱한 후 다음 노드로 전달한다.
5.2.2 연쇄법칙이란
합성 함수 : 여러 함수로 구성된 함수.
\[z=(x+y)^2\\ \downarrow\\ z=t^2\\ t=x+y\]합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
\[{\partial z\over \partial x}={\partial z\over \partial t}{\partial t\over \partial x}\] \[{\partial z\over \partial x}={\partial z\over \cancel{\partial t}}{\cancel{\partial t}\over \partial x}\]- 국소적 미분(편미분) 계산
- 연쇄법칙$\mathsf{^{chain rule}}$ 적용
5.2.3 연쇄법칙과 계산 그래프
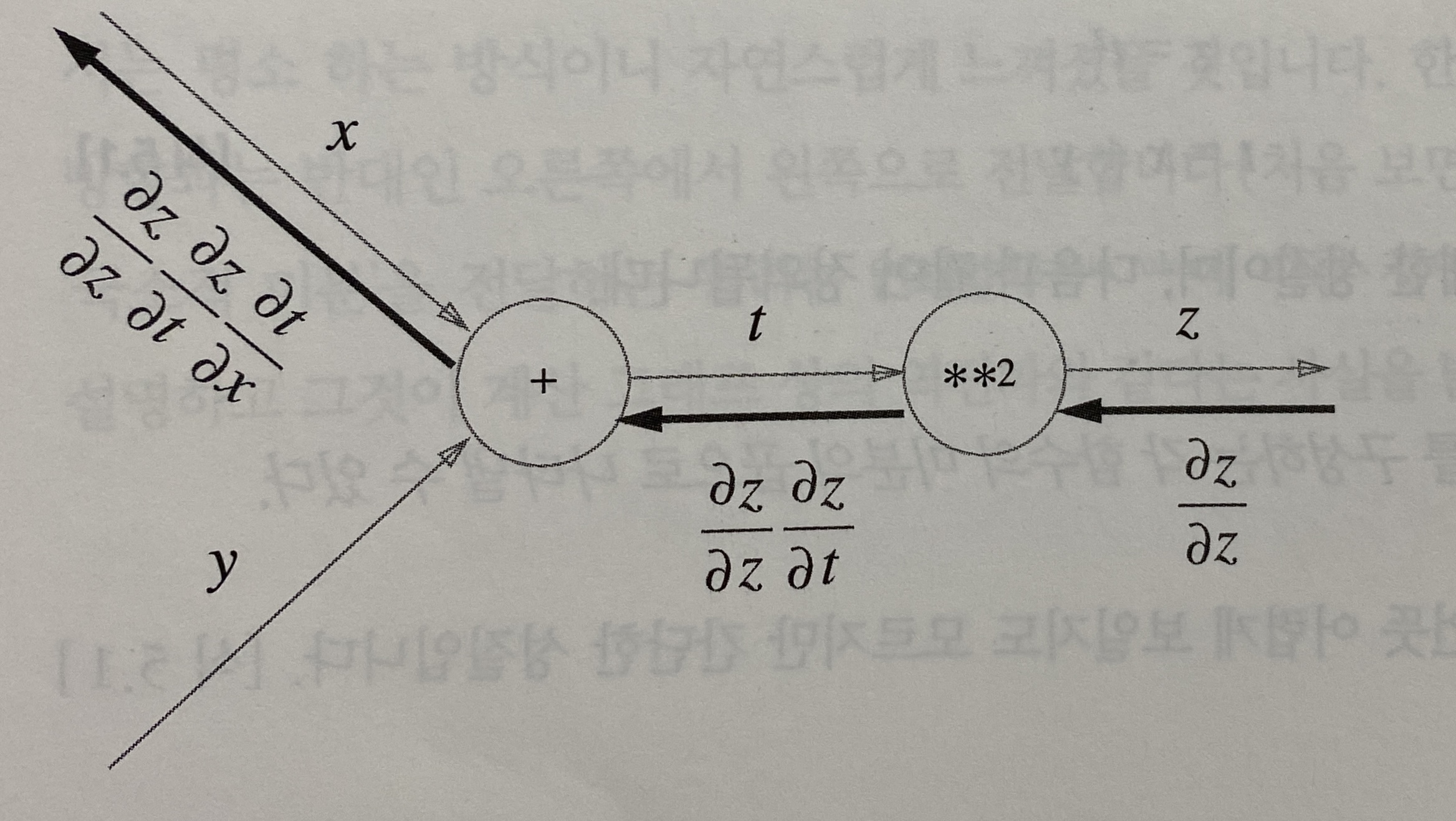
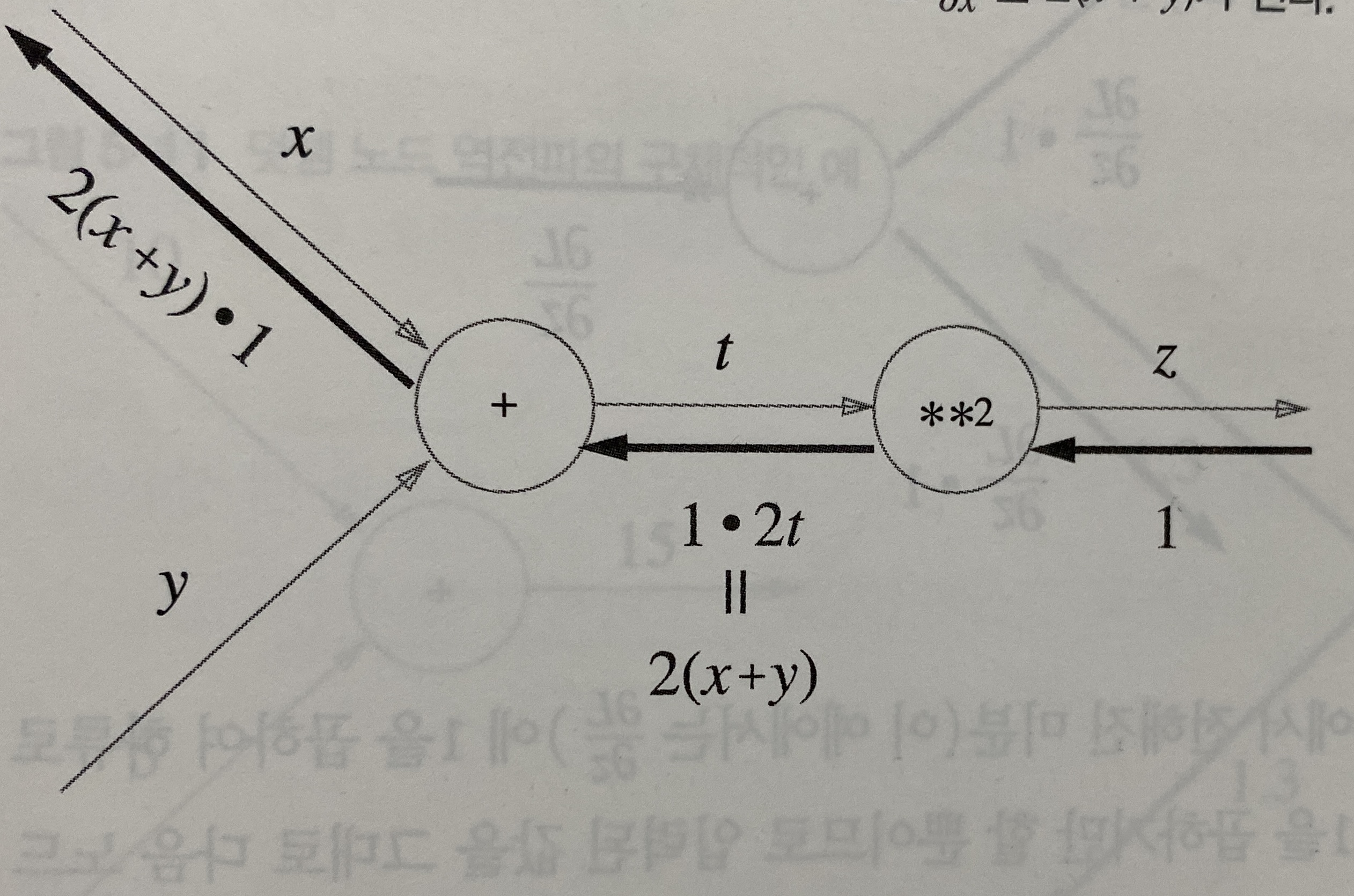
역전파 방향으로 국소적 미분을 곱하면 입력에 대한 출력의 미분값을 계산한것과 같다.
5.3 역전파
5.3.1 덧셈 노드의 역전파
\[z=x+y\] \[{\partial z\over\partial x}=1\] \[{\partial z\over\partial y}=1\]x, y : 덧셈노드의 입력
z : 덧셈노드의 출력
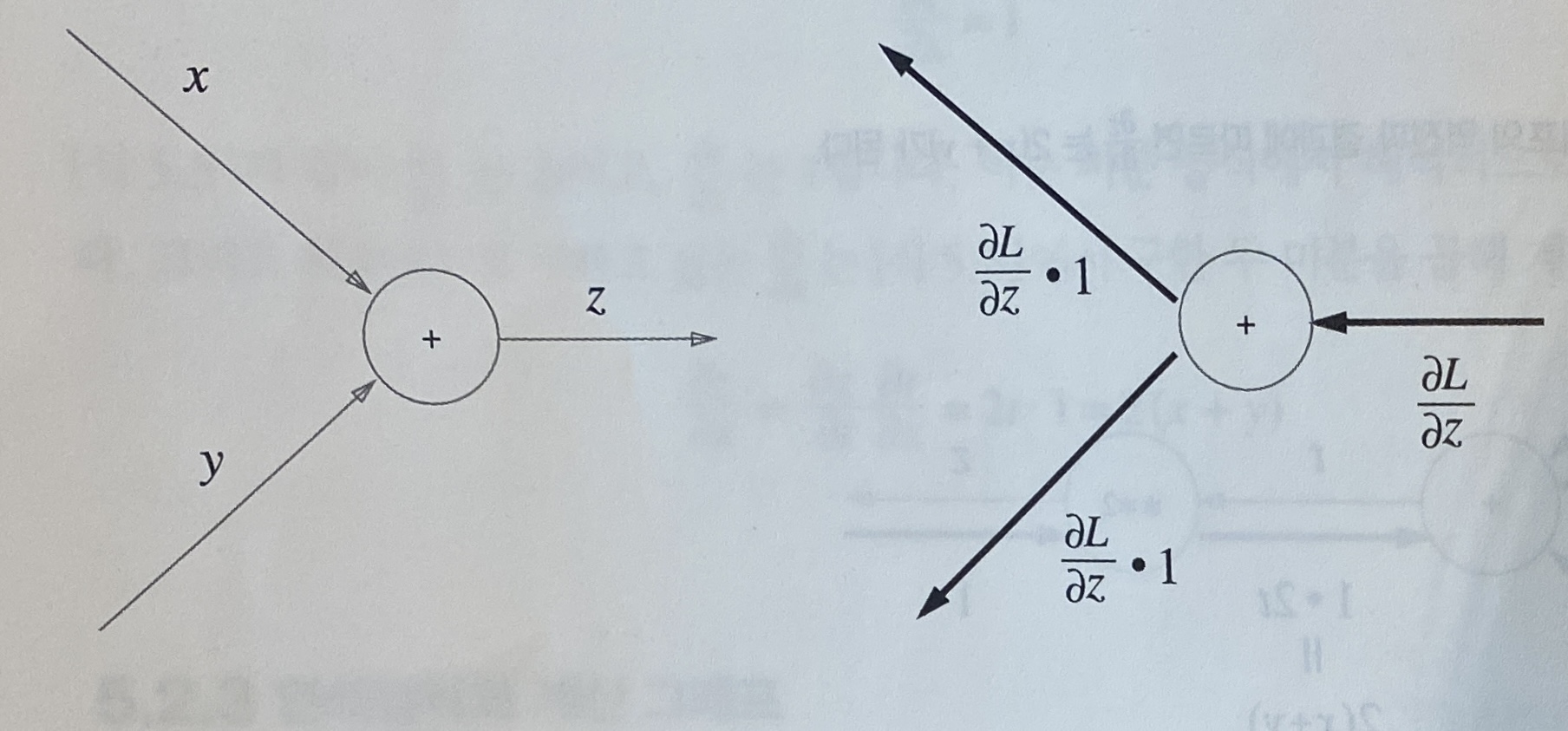
앞에 임의의 계산이 있더라도 연쇄법칙에 의해 덧셈노드의 상류에서 흘러온 미분 값은 $\partial L\over\partial z$가 된다.
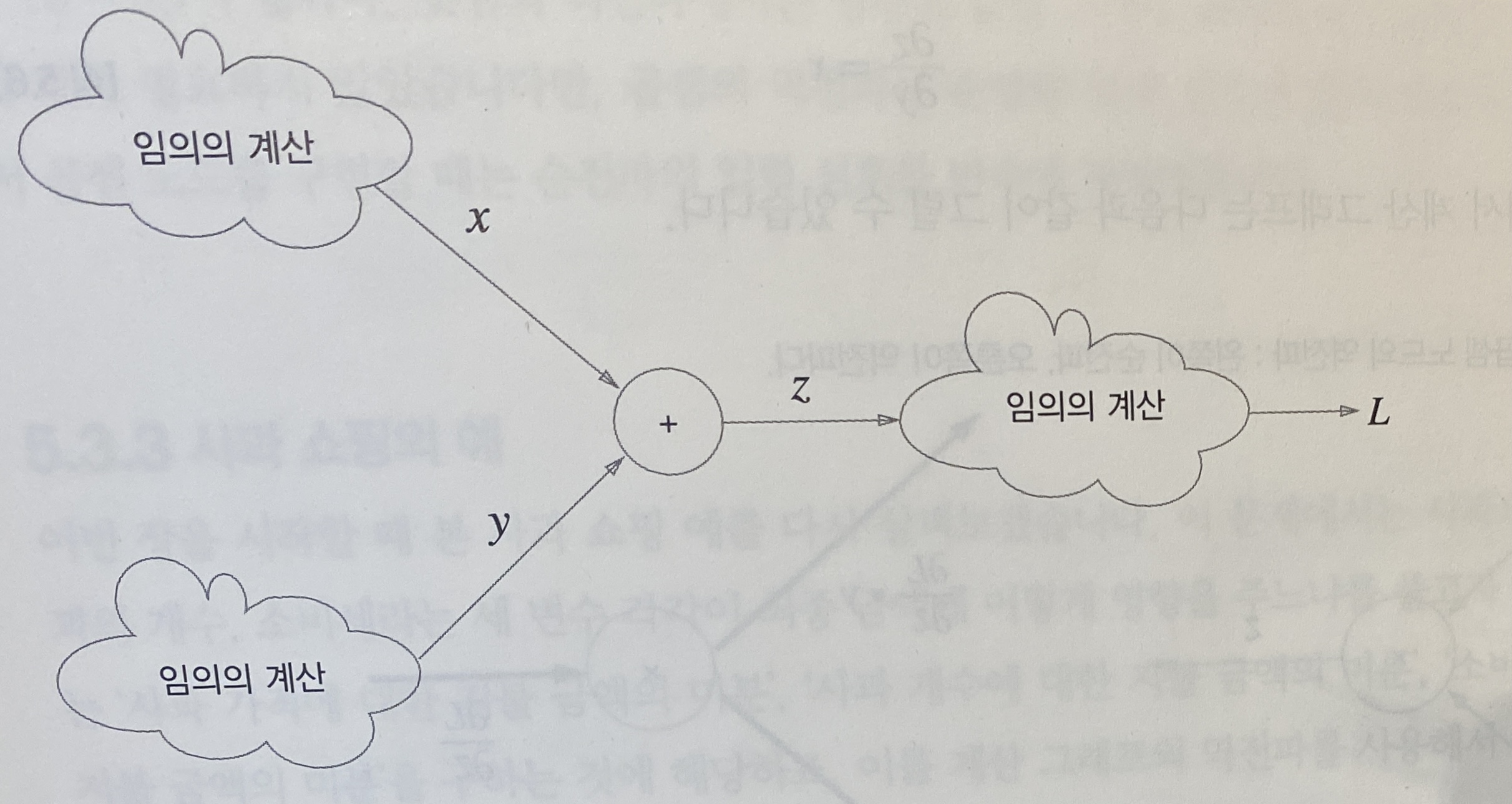
5.3.2 곱셈 노드의 역전파
\[z=xy\] \[{\partial z\over\partial x}=y\] \[{\partial z\over\partial y}=x\]곱셈노드의 각 입력에 의한 미분 값은 자신이 아닌 다른 입력값
따라서 입력 x에 의한 출력의 미분 값은 ${\partial L\over\partial z}\cdot y$
입력y에 의한 출력의 미분 값은 ${\partial L\over\partial z}\cdot x$
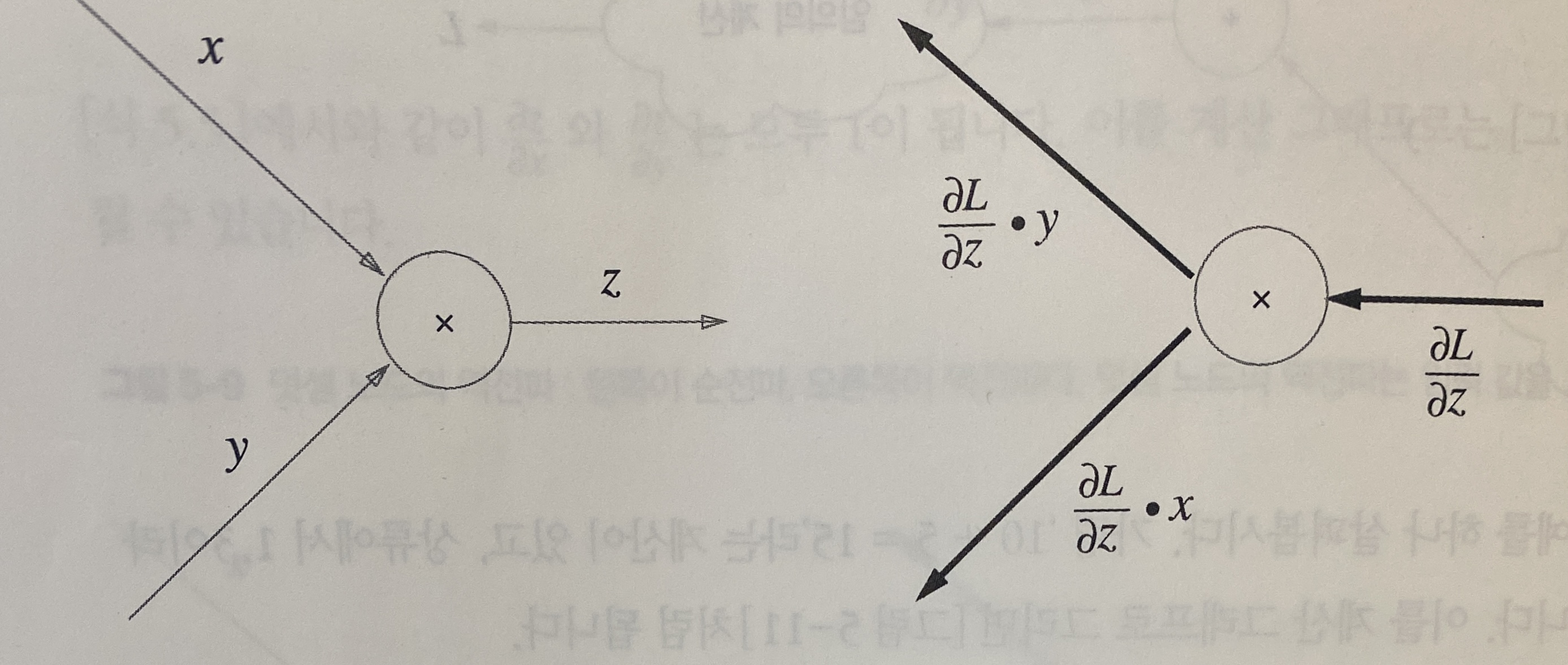
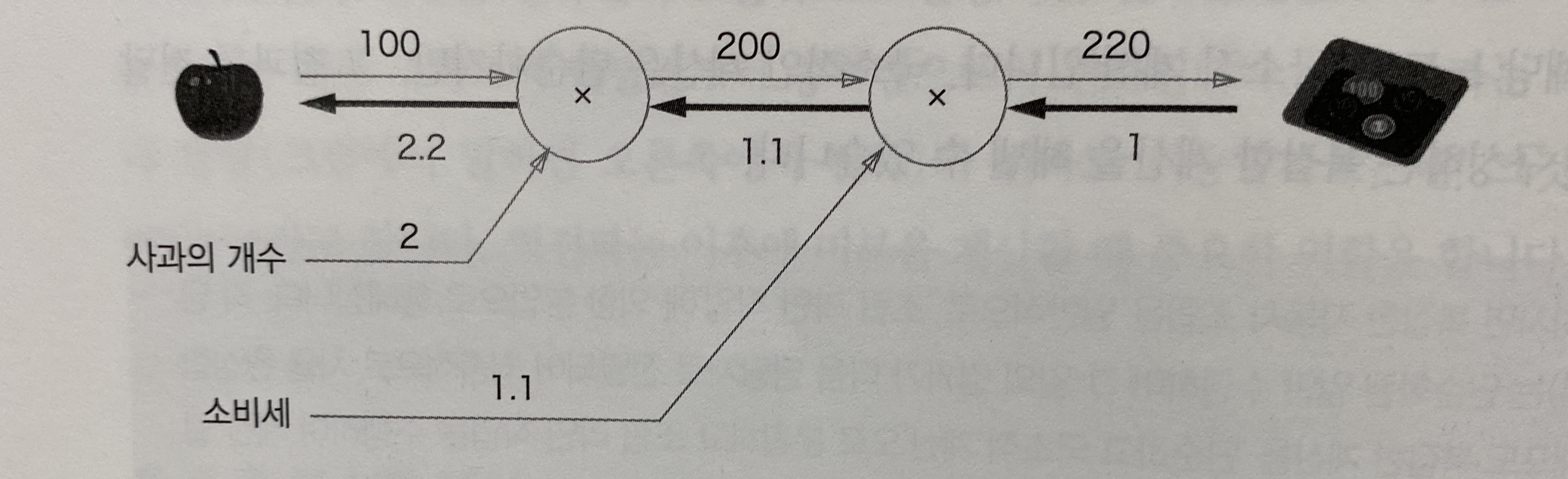
5.3.3 사과 쇼핑의 예
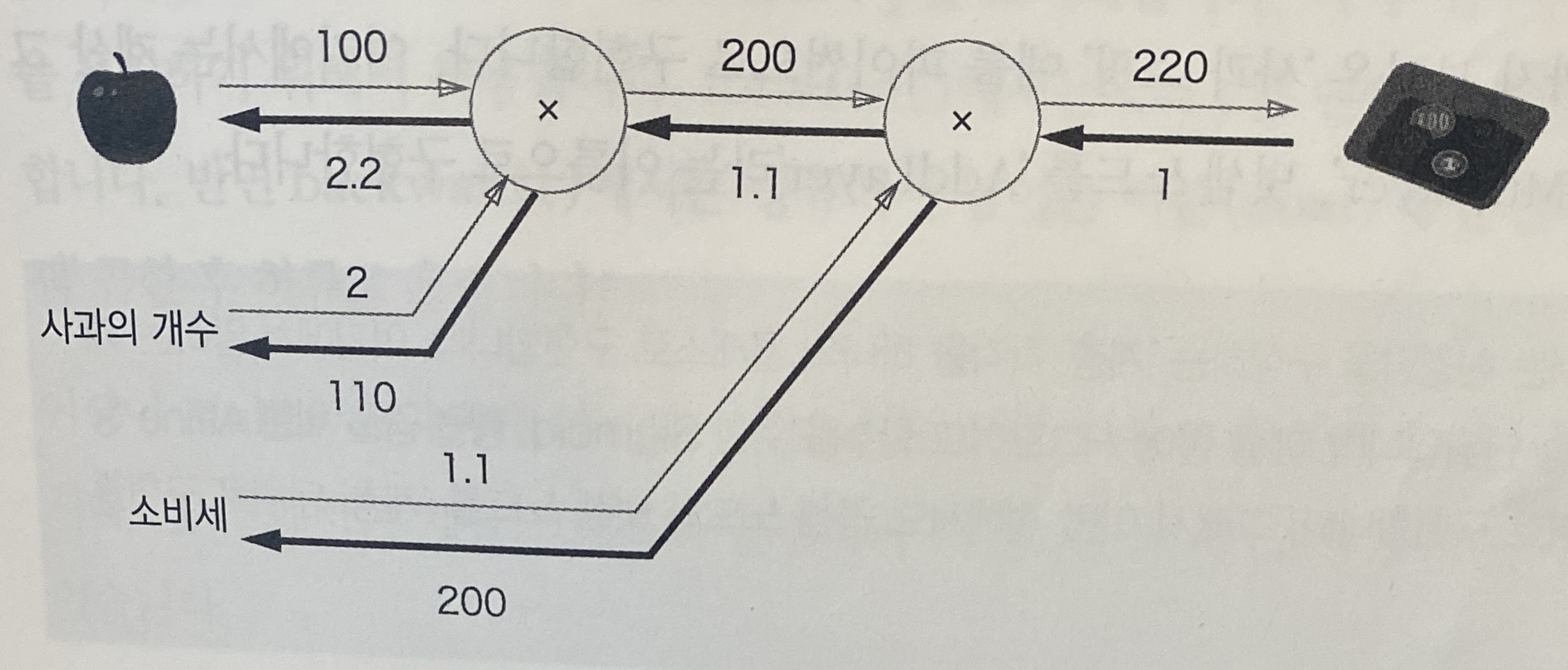
5.4 단순한 계층 구현하기
계산 그래프를 파이썬으로 구현해보는 절
5.4.1 곱셈 계층
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self,x,y):
self.x = x
self.y = y
out = x*y
return out
def backward(self,dout):
dx = dout * self.y
dy = dout * self.x
return dx, dy
5.4.2 덧셈 계층
class AddLayer:
def __init__(self):
pass
def forward(self,x,y):
out = x+y
return out
def backward(self,dout):
dx = dout*1
dy = dout*1
return dx, dy
5.5 활성화 함수 계층 구현하기
활성함수 ReLu와 sigmoid 계층 구현
5.5.1 ReLu 계층
\[y=\begin{cases} x & (x>0)\\ 0 & (x\le0) \end{cases}\] \[{\partial y\over\partial x}=\begin{cases} 1 & (x>0)\\ 0 & (x\le0) \end{cases}\]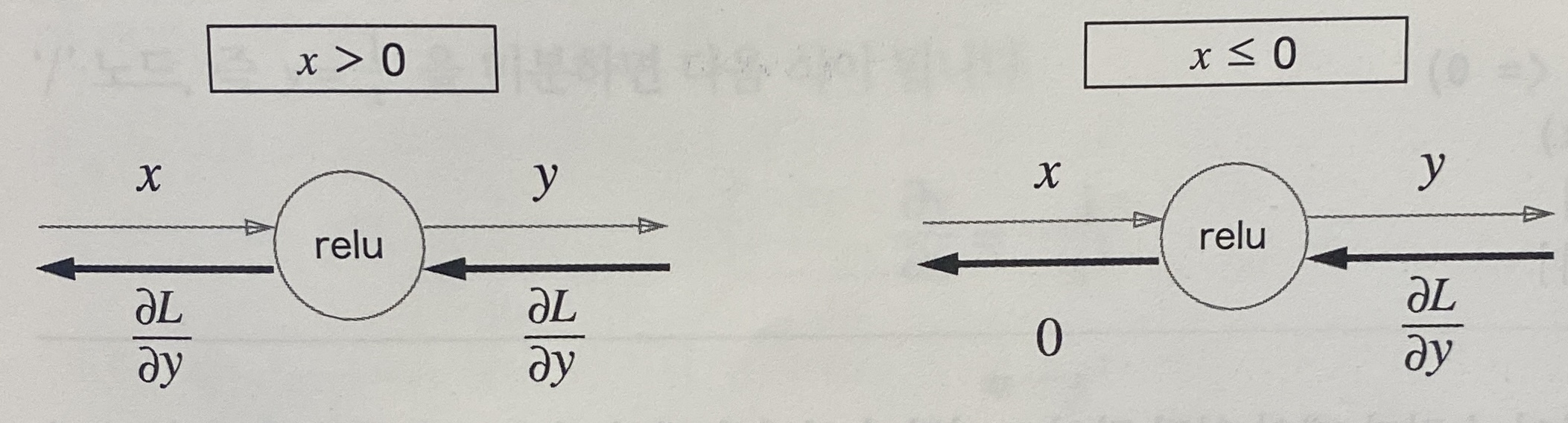
class ReLu:
def __init__(self):
self.mask = None
def forward(self,x):
self.mask = (x<=0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
ReLu 계층은 전기 회로의 ‘스위치’에 비유할 수 있다.
순전파 때 전류가 흐르고 있으면$(x>0)$ 스위치를 ON으로 하고, 흐르지 않으면$(x\le0)$ OFF로 한다.
역전파 때는 스위치가 ON이라면 전류가 그대로 흐르고, OFF면 더 이상 흐르지 않는다.
5.5.2 Sigmoid 계층
\[y={1\over1+e^{-x}}\]아래 sigmoid 함수의 계산 그래프를 보면
덧셈 노드, 곱셈 노드, ‘exp’ 노드와 ‘ / ’ 노드가 사용된다.
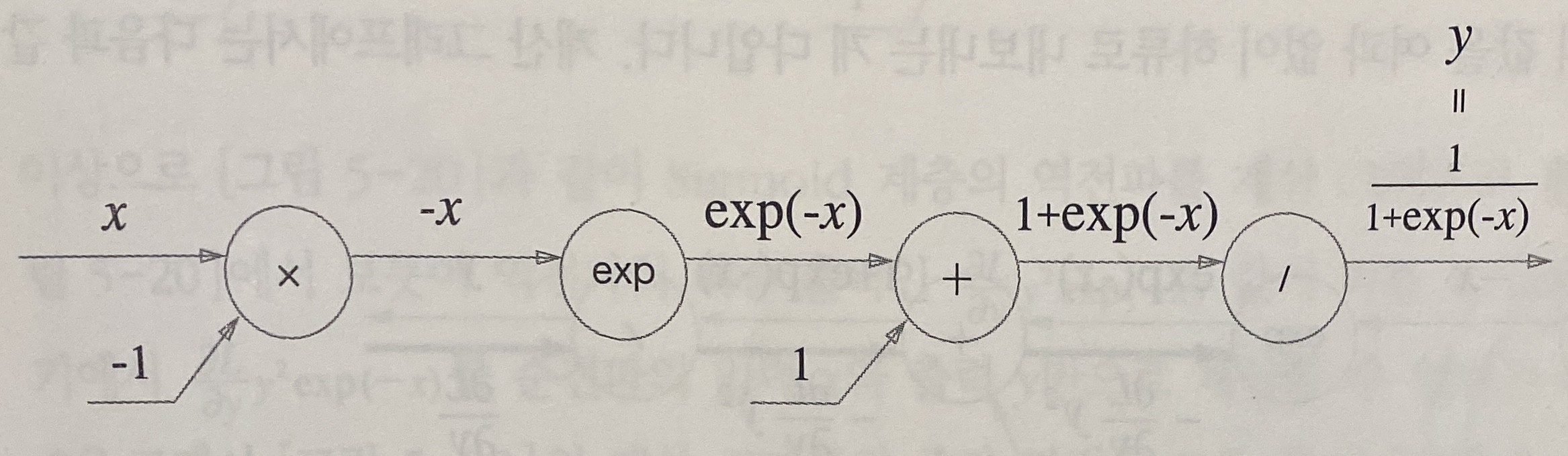
sigmoid 함수의 역전파 과정
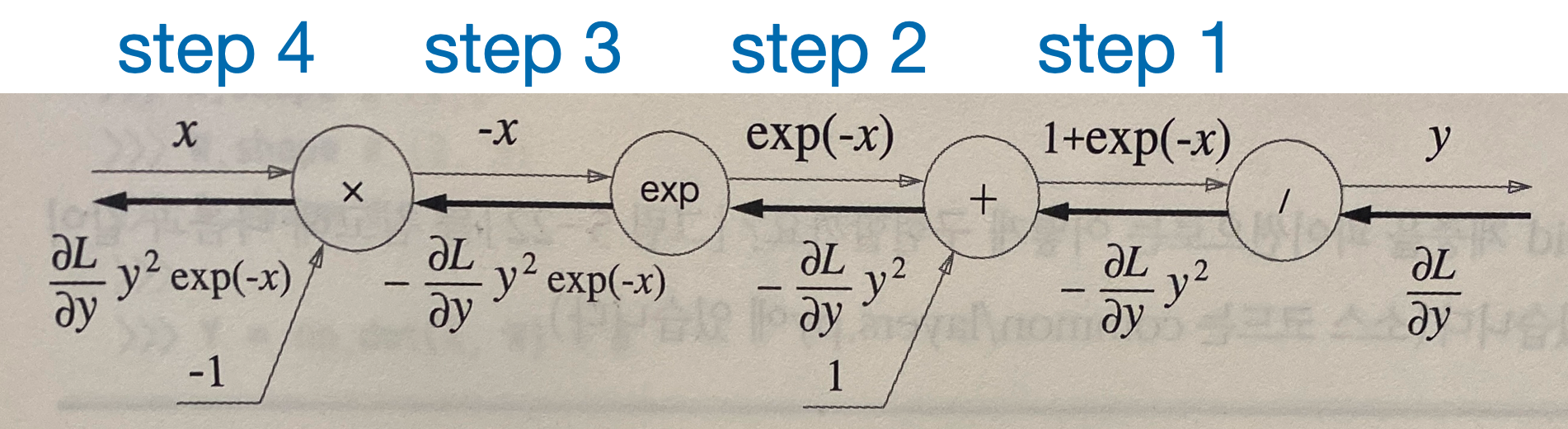
step 1 결과 : $-{\partial L\over\partial y}\cdot y^2$
ex>
\[\begin{align*} y&={1\over x}\\ {\partial y\over\partial x}&=-{1\over\ x^2}\\ &=-y^2 \end{align*}\]step 2 결과 : $-{\partial L\over\partial y}\cdot y^2$
덧셈 노드는 상류의 값을 여과 없이 하류로 내보낸다.
ex>
\[\begin{align*} y&=x+1\\ {\partial y\over\partial x}&=1 \end{align*}\]step 3 결과 : $-{\partial L\over\partial y}\cdot y^2\cdot e^{-x}$
exp 노드의 편미분값은 원래 exp와 같다.
ex>
\[\begin{align*} y&=e^x\\ {\partial y\over\partial x}&=e^x \end{align*}\]주의할 점은 step 3에서 exp노드의 입력값이 $e^{-x}$이므로
역전파 계산시 exp노드를 통과하면 국소적 미분값으로 $e^{-x}$를 곱해야 한다.
step 4 결과 : ${\partial L\over\partial y}\cdot y^2\cdot e^{-x}$
곱셈 노드의 역전파 계산은 순전파 때의 값을 서로 바꿔 곱한다.
ex>
\[\begin{align*} y&=x\cdot c\\ {\partial y\over\partial x}&=c \end{align*}\]최종 결과
\[\begin{align*} {\partial L\over\partial y}\cdot y^2\cdot e^{-x}=&{\partial L\over\partial y}{1\over (1+e^{-x})^2}e^{-x}\\ =&{\partial L\over\partial y}{1\over1+e^{-x}}{e^{-x}\over1+e^{-x}}\\ =&{\partial L\over\partial y}\cdot y(1-y)\\ &(\because y={1\over1+e^{-x}}) \end{align*}\]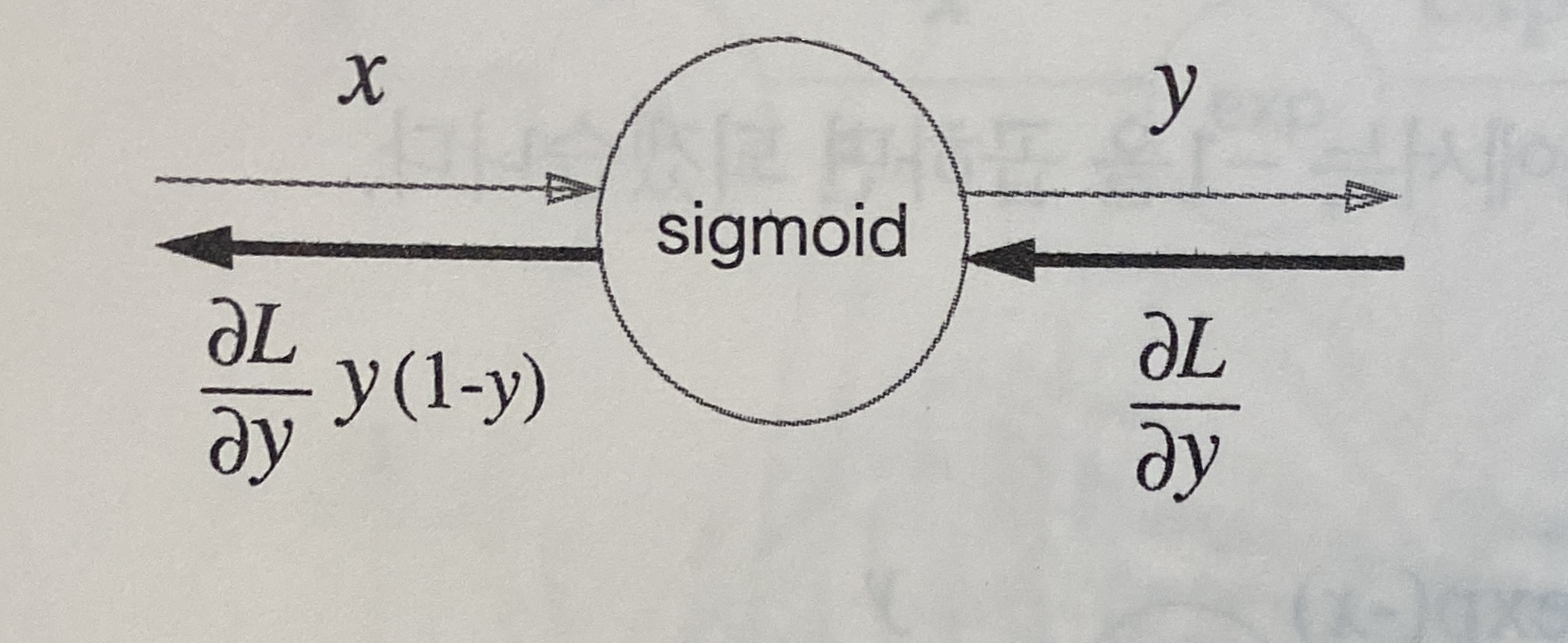
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1 - dout)
return dx
5.6 Affine/Softmax 계층 구현
*벡터의 미분
5.6.1 Affine 계층
신경망의 순전파 때 수행하는 행렬의 곱은 기하학에서는 어파인 변환$\mathsf{^{affine\ transformation}}$이라고 한다.
Affine 계층의 계산 그래프 : 변수가 행렬임에 주의, 각 변수의 형상을 변수명 위에 표기했다.
이제부터는 노드 사이에 벡터와 행렬도 흐른다.
dot노드의 역전파는 곱셈 노드의 역전파와 개념이 같은데 계산되는 변수가 다차원 배열이기 때문에 서로 도트곱을 할 수 있도록 차원을 맞춰줘야 한다.
\[\begin{align*} &{\partial L\over\partial X}=& {\partial L\over\partial Y}\cdot &W^T\\ &(2,)&(3,)\cdot&(3,2)\\&\\ &{\partial L\over\partial W}=& X^T\cdot&{\partial L\over\partial Y}\\ &(2,3)&(2,1)\cdot&(,3) \end{align*}\]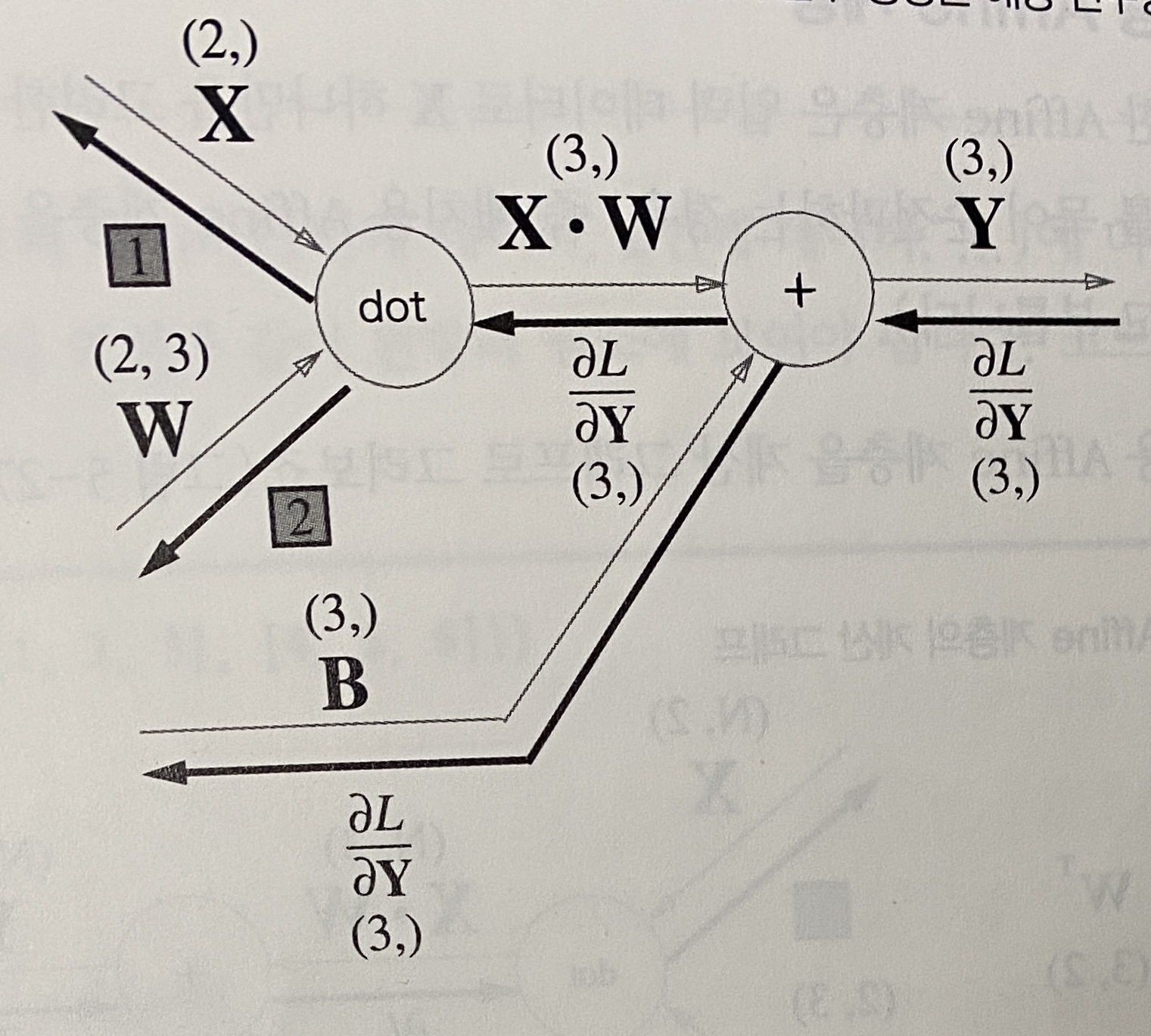
5.6.2 배치용 Affine 계층
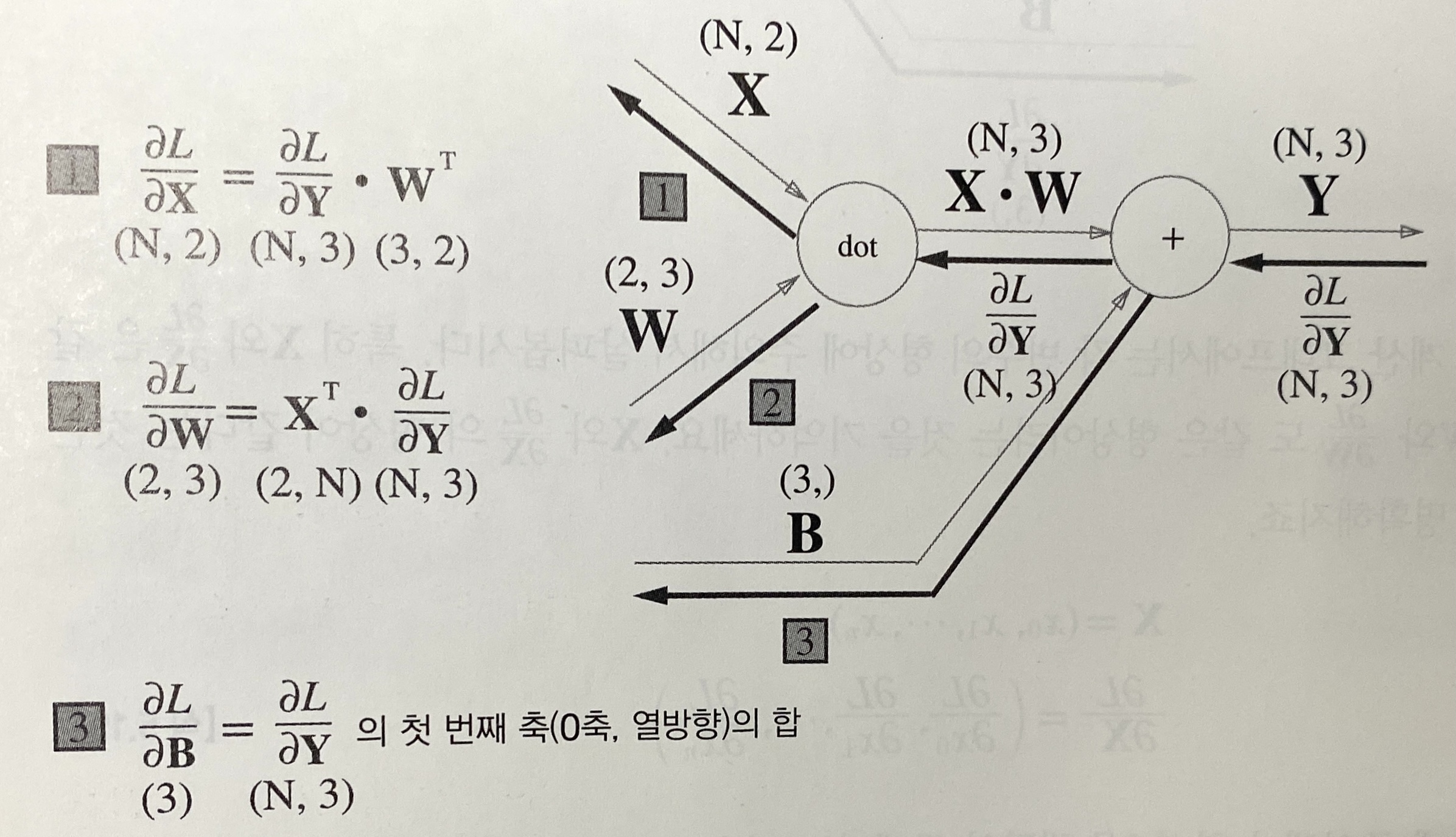
순전파의 편향 덧셈은 각각의 데이터( 1 번째 데이터, 2번째 데이터, …)에 더해진다.
그래서 역전파 때는 각 데이터의 역전파 값이 편향의 원소에 모여야 한다.
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
self.dW = None
self.db = None
def forward(self, x):
self.original_x_shape = x.shape
x = x.reshape(x.shape[0],-1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self,dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape)
return dx
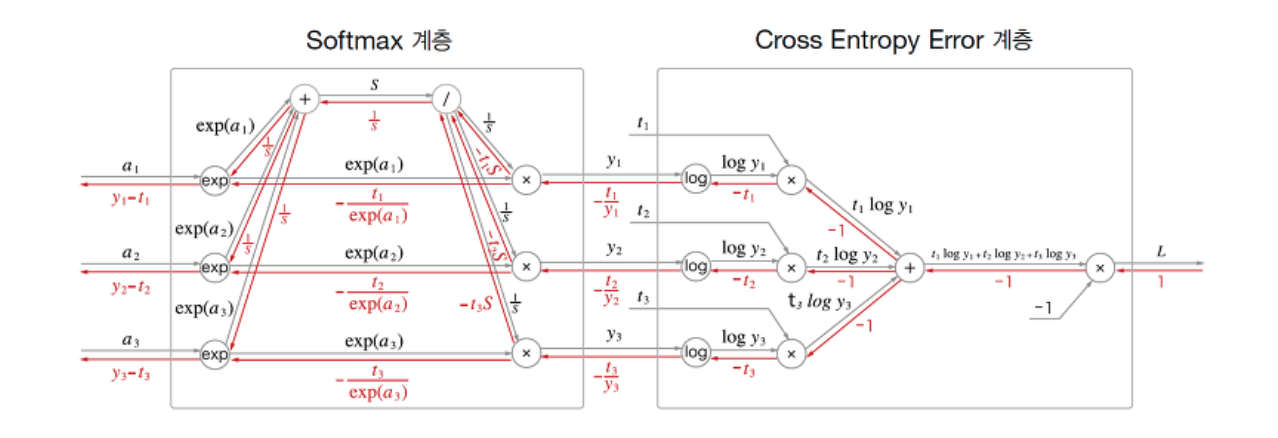
5.6.3 Softmax-with-Loss Layer
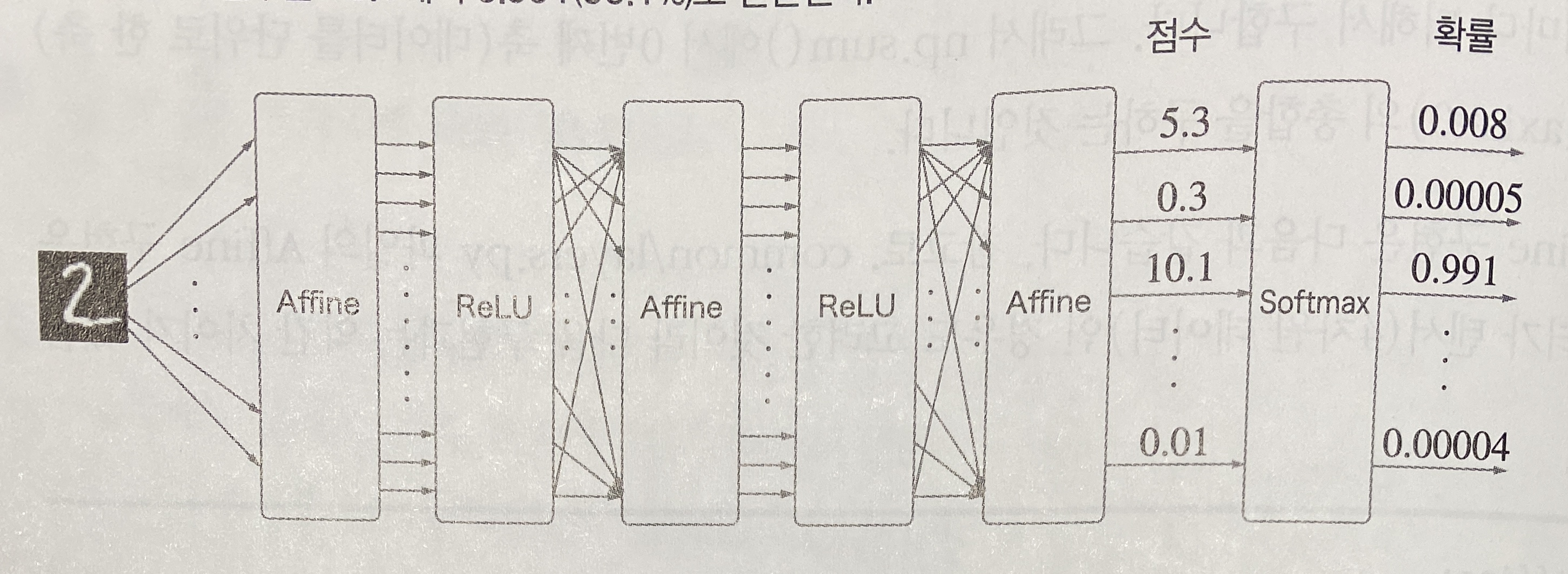
손글씨 숫자 인식에서의 softmax 계층의 출력의 모습인데
0~9까지 10개의 숫자를 분류하기 때문에 입력도 10개고 출력도 10개다
softmax계층을 cross entropy error계층과 함께 구현한다.
Forward Propagation
1. Softmax
\[\begin{align*} y_k&={e^{a_k}\over\sum\limits_i^ne^{a_i}}\\ S&=e^{a_1}+e^{a_2}+e^{a_3}\\ y_1&={e^{a_1}\over S}\quad y_2={e^{a_2}\over S}\quad y_3={e^{a_3}\over S} \end{align*}\]
2. Cross Entropy Error
\[L=-\sum\limits_kt_k\log(y_k)\]
Back Propagation
1. Cross Entropy Error
\[y=\log x\\ {\partial y\over\partial x}={1\over x}\]
2. Softmax
step 1
step 2
step 3
순전파 때 여러 갈래로 나뉘어 흘렸다면 역전파 때는 그 반대로 흘러온 여러 값을 더한다.
step 4
step 5
step 6
결과
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx
5.7 오차역전파법 구현하기
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size,\
weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
self.layers = OrderedDict()
self.layers['Affine1'] = \
Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = ReLu()
self.layers['Affine2'] = \
Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
self.loss(x, t)
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads
5.7.3 오차역전파법으로 구한 기울기 검증하기
기울기를 구하는 방법으로
- 수치 미분
- 해석적 미준
두가지를 알았다.
계산 그래프를 통해 해석적 미분을 계산하면서
느린 수치 미분보다 효율적 결과를 얻을 수 있다.
| 수치 미분 | 해석적 미분 | |
|---|---|---|
| 속도 | 느림 | 빠름 |
| 구현 난이도 | 쉬움 | 어려움 |
때문에 수치 미분 값과 오차역전파법의 결과를 비교하여 제대로 구현 되었는지 확인한다. → 기울기 확인$\mathsf{^{gradient\ check}}$