Ch4 신경망 학습
Ch4 신경망 학습
학습
훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것을 뜻함
신경망이 학습하는 것을 나타내는 지표로 손실 함수를 사용한다.
이 때 손실 함수의 값이 작을수록 학습이 잘 된것이라 한다.
4.1 데이터에서 학습한다.
신경망의 특징은 데이터를 보고 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 것이다.
4.1.1 데이터 주도 학습
학습 파이프라인의 전환
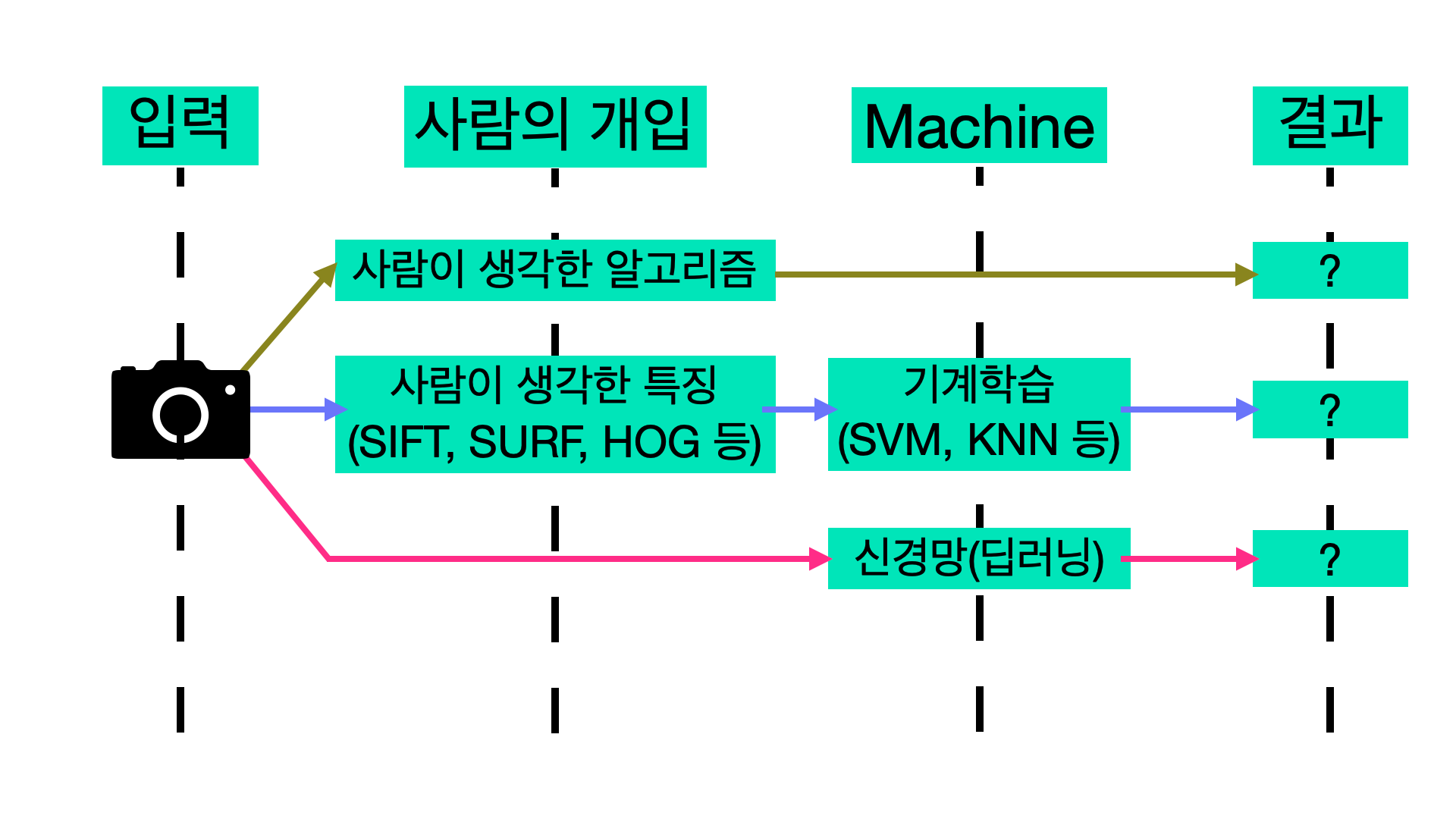
- 첫 번째 방법에서는 알고리즘을 만들어내기 매우 어려움
- 두 번째 기계학습을 통해 효율을 높였지만 여전히 사람이 특징을 적절하게 뽑아야함
-
세 번째 방법에서는 신경망이 직접 데이터를 통해 학습한다.
따라서 숫자5를 인식하는 문제든 강아지를 인식하는 문제든 사람의 얼굴을 인식하는 문제든
사람의 개입없이 문제를 해결할 수 있음 ( end-to-end machine learning )
4.1.2 훈련 데이터와 시험 데이터
학습에 사용하는 데이터는 훈련 데이터(training data)와 시험 데이터(test data)로 나뉜다.
좋은 모델은 새로운 데이터로도 문제를 올바르게 풀어내는 능력이 중요하기 때문에
모델을 평가할 때는 학습에 사용된 훈련 데이터말고 훈련에 사용되지 않은 시험 데이터로 평가한다.
갖고 있는 모든 데이터를 학습 데이터로 사용하면 데이터셋에 Overfitting이 일어나도 확인 할 수 없다.
4.2 손실 함수 ( Loss Function )
신경망의 성능을 나타내는 지표를 손실 함수라 하고
오차제곱합( Sum of Squares for error, SSE )과 교차 엔트로피 오차( Cross Entropy Error, CEE )가 일반적
4.2.1 오차제곱합 ( SSE )
\[\begin{align*}E=&\frac{1}{2}\sum\limits_k(y_k-t_k)^2\\ y_k\ &:\ \mathsf{output}\\ t_k\ &:\ \mathsf{answer\ \ label}\\ k\ &:\ \mathsf{dimension\ \ of\ \ data}\end{align*}\]*one-hot encoding
한 원소만 1로하고 그 외는 0으로 나타내는 표기법
4.2.2 교차 엔트로피 오차 ( CEE )
\[\begin{align*}E=&-\sum\limits_kt_k\log(y_k)\\ y_k\ &:\ \mathsf{output}\\ t_k\ &:\ \mathsf{answer\ \ label\ (one-hot\ \ encoding)}\\ k\ &:\ \mathsf{dimension\ \ of\ \ data}\end{align*}\]4.2.3 미니배치 학습
기계학습은 훈련 데이터를 사용해 학습한다.
훈련 데이터에 대한 손실 함수의 값을 구하고, 그 값을 최대한 줄여주는 매개변수를 찾아낸다.
따라서 모든 훈련 데이터를 대상으로 오차를 구하고 그 합을 지표로 삼는다.
( 훈련 데이터가 1000개면 1000번의 손실 함수를 실행해야함 )
빅데이터 수준에서는 데이터의 수가 수백만개 수천만개가 넘기 때문에
데이터 전체에 대한 손실 함수를 계산하기 어렵기 때문에 일부(미니배치$\mathsf{^{mini-batch}}$)만 골라서 학습.
이렇게 학습하는 방법을 미니배치 학습 이라고 한다.
4.2.4 (배치용) 교차 엔트로피 오차
평균 손실 함수
\[\begin{align*} E&=-\frac{1}{N}\sum\limits_n\sum\limits_kt_{nk}\log y_{nk}\\ \mathsf{N}\ &:\ \mathsf{the\ \ number\ \ of\ \ Data}\\ t_{nk}\ &:\mathsf{\ k_{th}\ answer\ of \ \ n_{th}\ \ data}\\ y_{nk}\ &:\mathsf{\ k_{th}\ output\ of\ \ n_{th}\ \ data} \end{align*}\]N으로 나눠서 정규화하면
- 범위를 0~1로 조절
- 훈련 데이터의 개수와 관계없이 통일된 지표를 얻음
4.2.5 왜 손실 함수를 설정하는가?
신경망 학습의 궁극적인 목표는 높은 정확도 이지만
학습 방법으로 정확도를 지표로 사용하지 않고 손실 함수를 사용한다.
학습을 통해 신경망에 사용되는 매개변수를 조절할 때 미분 값을 사용하는데
정확도를 지표로 삼는 함수의 미분 값은 대부분의 장소에서 0이되어 매개변수 조절이 불가능하기 때문이다.
또한, 정확도는 매개변수의 변화에 의해 값이 이산적으로 변하는데
그것은 매개변수의 변화가 주는 변화를 정확도가 무시하고 있다는 것입니다.
반면 손실 함수는 미분 값이 0인 경우 학습이 종료되고 매개변수의 변화에 의해 손실 함숫값은 연속적으로 변해
매개변수 변화에 민감하게 반응해 최적의 매개변수를 구하기 좋다.
같은 맥락에서 step 함수를 활성 함수로 쓰지 않는다.
step 함수는 대부분의 장소에서 미분 값이 0이고 그 함숫값이 이산적이어서
모델의 학습 지표를 손실 함수로 삼는다 하더라도 학습이 되지 않기 때문이다.
4.3 수치 미분
경사법에서는 기울기(미분 값)을 기준으로 매개변수를 조절한다.
4.3.1 미분
미분이란 한순간의 변화량
전방 차분 ( Forward Difference )
\[\begin{align*} \dfrac{d\ f(x)}{dx}=\lim_{h\rightarrow 0}\dfrac{f(x+h)-f(x)}{h} \end{align*}\]위와 같은 미분 방법을 전방 차분이라 하고 수치 미분법 중 하나이다.
또 다른 수치 미분법으로는
중앙 차분( Central Difference )
\[\begin{align*} \dfrac{d\ f(x)}{dx}=\lim_{h\rightarrow 0}\dfrac{f(x+h)-f(x-h)}{2h} \end{align*}\]후방 차분 ( Backward Difference )
\[\begin{align*} \dfrac{d\ f(x)}{dx}=\lim_{h\rightarrow 0}\dfrac{f(x)-f(x-h)}{h} \end{align*}\]사람이 직접 수학 문제를 풀 때 사용하는 전개해서 미분하는 방법을 해석적 미분이라고 하는데
\[\begin{align*} y=x^2 \\{dy \over dx}=2x \end{align*}\]이런 해석적 미분은 전개식을 통해 미분하는데 프로그래밍 할 때는
- 함수를 정의했을 경우 그 함수의 전개식을 따로 저장해둬야 한다. (ex> string)
그래도 미분을 위해 전개식을 string으로 저장했다 하더라도 정규 문법을 정하기 어렵다.
- 다변수 함수까지 처리하려면 정규 문법을 정하는 것도 쉽지않다.
때문에 오차 값을 감안하고 프로그래밍 할 때는 수치 미분을 한다.
해석적 미분을 하면 참값이 나오지만 수치 미분을 하면 오차가 생길 수밖에 없다.
그래서 그 오차를 최대한 줄이기 위해서는 차분의 간격을 최대한 좁히는 것이다.
그렇게해서 구현을 하게 되면 아래와 같은데 먼저 잘못된 예를 보면
def bad_numerical_diff(f,x):
h = 1e-50
return (f(x+h) - f(x)) / h
차분의 간격을 줄이려고 h값을 너무 작게 설정하면
python이 그 값을 반올림을 해서 그 값이 무시되는(0으로 되는) 반올림 오차$\mathsf{^{rounding\ error}}$가 발생한다.
따라서 h값은 $10^{-4}$정도의 값으로 사용한다.
그리고 차분은 두 점의 기울기 값 이기고 3개의 방법 중 중앙 차분을 이용해 구현해 보면 아래와 같다.
def central_numerical_diff(f,x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
4.3.2 수치 미분의 예
\[y=0.01x^2+0.1x\]def function_1(x):
return 0.01*x**2 + 0.1*x
4.3.3 편미분
\[f(x_0,\ x_1)=x^2_0+x^2_1\]def function_2(x):
return x[0]**2 + x[1]**2
# or return np.sum(x**2)
# x0=3, x1=4 일 때, x0에 대한 편미분
def function_tmp1(x0):
return x0*x0 + 4.0**2.0
# x1에 대한 편미분
def function_tmp2(x1):
return 3.0**2.0 + x1*x1
편미분 하려는 변수를 제외한 나머지 변수는 고정값을 대입하여
새로운 함수를 정의한다.
4.4 기울기
한 함수를 통해 모든 변수에 대한 편미분 결과를 벡터로 정리한 것을 기울기$\mathsf{^{gradient}}$라고 한다.
def numerical_gradient(f,x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
return grad
기울기가 가리키는 쪽은 각 장소에서 함수의 출력 값을 가장 크게 줄이는 방향
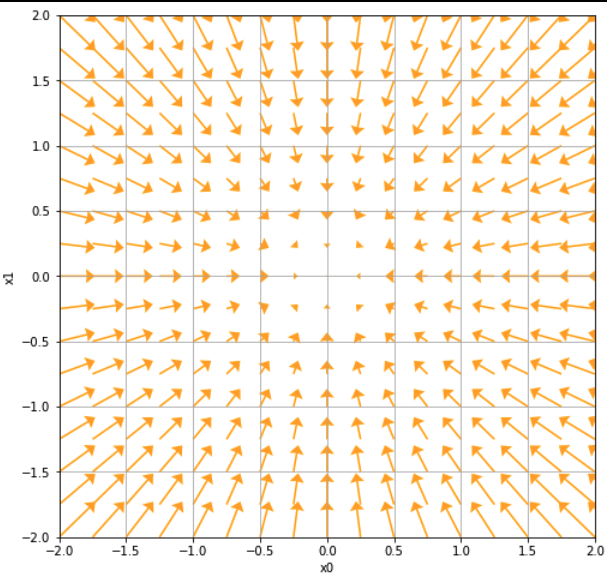
*잘못된 함수 구현
결과의 차이는 없지만 제대로 구하는 건 아니라 생각
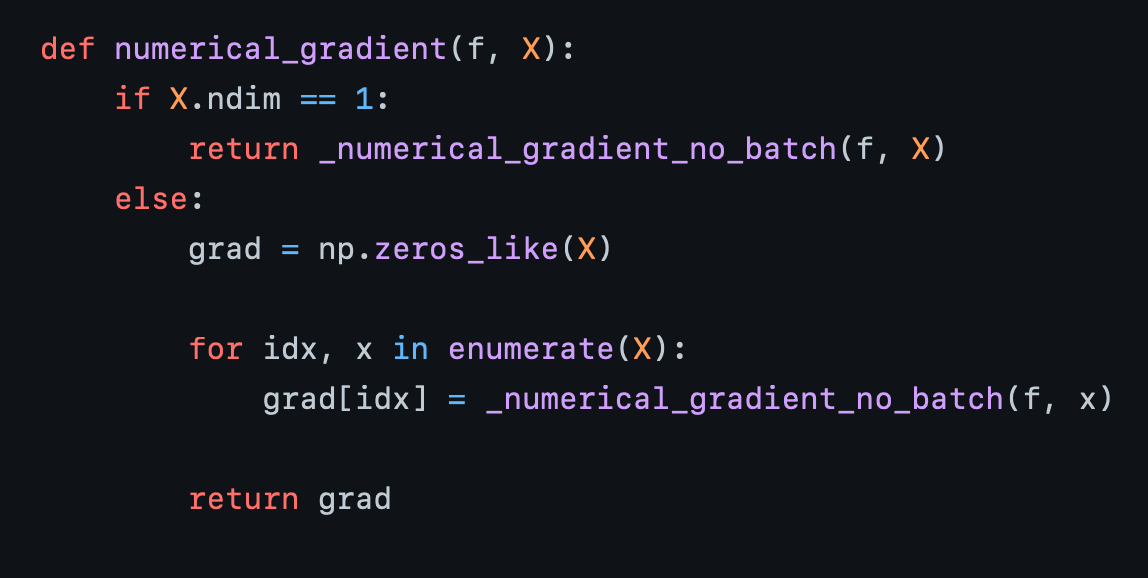

4.4.1 경사법( Gradient method )
광대한 매개변수 공간에서 어디가 손실함수를 최솟값으로 만드는 곳인지
기울기를 이용여 찾는 방법
기울기를 지표로 최적의 매개변수를 찾으러 움직이지만
기울기가 가리키는 곳에 정말 함수의 최솟값이 있는지는 보장되지 않는다.
함수의 기울기가 0인 지점은 최솟값, 극솟값, 안장점이 될 수 있다.
복잡하고 찌그러진 모양의 함수라면 평평한 곳으로 파고들면서 고원$\mathsf{^{plateau,플라토}}$라 하는 학습 정체기에 빠질 수 있다.
기울기의 방향이 반드시 최솟값을 가리키지는 않지만
그 방향으로 가야 함수의 값을 줄일 수 있다.
경사법에는 경사 하강법$\mathsf{^{gradient\ descent\ method}}$과 경사 상승법$\mathsf{^{gradient\ ascent\ method}}$이 있는데
기울기가 가리키는 방향으로 일정 거리만큼 이동하면서 함수의 값을 점차 줄여나가는 방법을 경사 하강법이라 한다.
\[\begin{align*} x_0&=x_0-\eta{\partial f\over\partial x_0}\\ x_1&=x_1-\eta{\partial f\over\partial x_1}\\ \eta&\ :\ \mathsf{learning\ rate} \end{align*}\]에타는 학습률을 뜻하는데 기울기 방향으로 이동할 거리를 조절하고
에타가 너무 크면 빠른 학습을 하지만 최솟값에 수렴하지 못할 수도 있고
에타가 너무 작으면 학습 속도가 너무 느려 시간 비용이 크게 들어가서
조절하면서 학습을 진행한다.
경사 하강법
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x -= lr*grad
return x
f : 최적화 하려는 함수
init_x : 학습을 시작할 위치
step_num : 경사법 반복 수
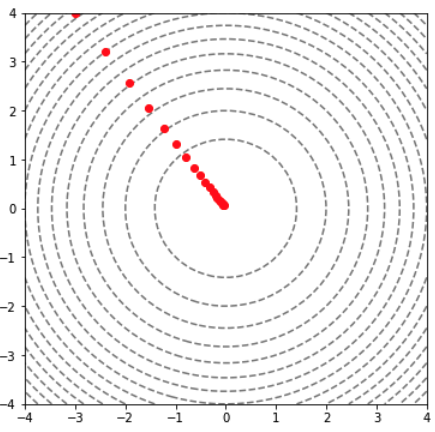
학습률 같은 매개변수를 하이퍼파라미터$\mathsf{^{hyper\ parameter,\ 초매개변수}}$라고 한다.
학습 과정에서 스스로 값이 설정되는 매개변수인 가중치와 편향과 달리
하이퍼파라미터는 사람이 직접 조절하면서 잘 맞는 값을 찾아야 한다.
4.4.2 신경망에서의 기울기
가중치 $W$, 손실함수 $L$인 신경망에서
\[\begin{align*} W&=\begin{pmatrix} w_{11}&w_{12}&w_{13}\\ w_{21}&w_{22}&w_{23} \end{pmatrix}\\ {\partial L\over\partial W}&= \begin{pmatrix} {\partial L\over\partial w_{11}}&{\partial L\over\partial w_{12}}&{\partial L\over\partial w_{13}}\\{\partial L\over\partial w_{21}}&{\partial L\over\partial w_{22}}&{\partial L\over\partial w_{23}} \end{pmatrix} \end{align*}\]${\partial L\over\partial w_{11}}$는 $w_{11}$의 값을 변경했을 때 손실 함수 $L$이 얼마나 변화하는지를 나타낸다.
4.5 학습 알고리즘 구현하기
전체
신경망에는 적응 가능한 가중치와 편향이 있고
이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 ‘학습’이라고 한다.
신경망 학습은 4단계로 수행된다.
1단계 - 미니배치
훈련 데이터 중 일부를 무작위로 가져온다.
이렇게 선별한 데이터를 미니배치라 하며, 그 미니배치의 손실 함수를 줄이는것이 목표다.
2단계 - 기울기 산출
미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구한다.
기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시한다.
3단계 - 매개변수 갱신
가중치 매개변수를 기울기 방향으로 아주 조금 갱신한다.
4단계 - 반복
1~3단계를 반복한다.